Реальная математика в ОГЭ. Разбор задания №5

Ольга Шутова

Все девятиклассники боятся задания №5 ОГЭ по математике. Многие даже не пытаются его прочитать. А зря — с 5 заданием легко справиться, если знать алгоритм. Из этой статьи вы узнаете, что такое модуль «Реальная математика» в ОГЭ и как решить страшное 5 задание.

Что такое реальная математика в ОГЭ?

ОГЭ по математике начинается с пяти практических заданий. ФИПИ утверждает, что эти задания проверяют умение выполнять вычисления и преобразования, использовать приобретённые знания и умения в практической деятельности и повседневной жизни, строить и исследовать простейшие математические модели. Другими словами, эти задания проверяют, смогут ли ученики применить математику в реальной жизни.

В этом году я готовила ребят к ОГЭ по математике, и столкнулась с тем, что ученики решают все задания с 1 по 4, а пятое боятся даже прочитать. Многие девятиклассники уверены, что последнее задание из блока практических задач страшное и нерешаемое. К счастью, своих учеников я переубедила, теперь постараюсь переубедить и вас. Максимум за это блок можно получить 5 баллов.

Научим решать сложные задания ОГЭ
по математике на пробном уроке
в MAXIMUM

Какие бывают задания по реальной математике?

Для начала давайте познакомимся с заданиями №1-5 в ОГЭ по математике. Вот какие прототипы могут встретиться на экзамене:

• План домохозяйства. Этот прототип можно найти в демоверсии ОГЭ 2020, тут будет дан план домового участка или парка, с расположенными на нём объектами.
• План квартиры. Данный прототип похож на предыдущий, только работать придётся с планом квартиры и комнатами внутри этой квартиры.
• Баня и печь. В этом прототипе сюжет будет про баню, придётся делать различные вычисления для одной комнаты – парного отделения, а также подбирать печь по габаритам и стоимости.
• Лист бумаги. Вы будете работать с классическим листом формата А0, который разделён на меньшие форматы. Все вычисления придётся производить с листом бумаги.
• План местности. Будет дан план расположения различных деревень и дорог, по которым между этими деревнями можно перемещаться.
• Автомобильное колесо. На мой взгляд, это самый сложный прототип. Нужно будет работать с автомобильным колесом, которое состоит из диска и шины, а также разбираться в маркировке этих колёс.
• Телефонный тариф. Это задание полезно для учеников. Рано или поздно вы сами будете выбирать себе телефонный тариф, анализировать расход минут и гигабайтов интернета. Мне кажется, что это одно из самых интересных заданий 🙂

Как решать 5 задание ОГЭ по математике

Теперь мы знакомы со всеми сюжетами заданий по реальной математике. Можно приступать к разбору самого страшного задания — №5. Я хочу показать несколько заданий, и дать вам единый алгоритм. Самое интересное, что для решения этих пятых заданий даже не нужно знать само условие и то, что происходило в предыдущих четырёх пунктах.

Начнем с прототипа «План домохозяйства».

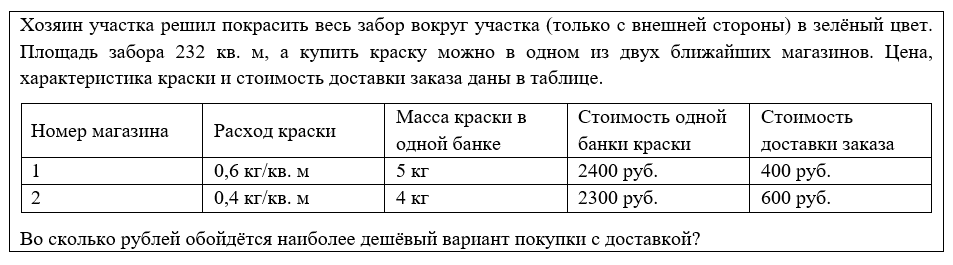
В этом задании нам нужно посчитать самый дешёвый вариант покраски забора с внешней стороны. Почему это задание так важно? Мы интуитивно всегда стараемся найти самый дешёвый вариант, чтобы мы ни делали. Нужен ли нам для этого сам план домохозяйства? Нет! Нужно ли нам опираться на то, что мы делали в заданиях 1-4? Нет! Именно поэтому это задание не такое страшное, каким кажется сначала.

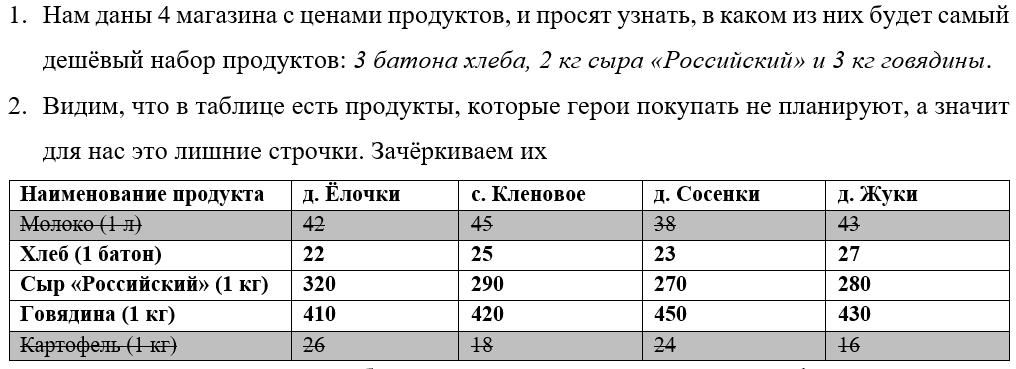
Чтобы успешно выполнить данное задание, нужно внимательно прочитать всё, что нам дано. Как правило, всю таблицу нужно использовать. а если там есть что-то лишнее, то это лишнее сразу же стоит зачеркнуть, чтобы не ошибиться. В нашем случае всего 2 варианта решения и никаких лишних данных, поэтому используем всё!

Нас просят сравнить два магазина и выбрать наиболее дешёвый вариант, для этого мы просчитаем стоимость покупки необходимого количества краски отдельно в каждом магазине.

Чтобы грамотно рассчитать необходимое количество банок краски, нужно расход краски умножить на площадь забора и разделить на массу краски в одной банке, таким образом мы получим количество банок, необходимое для покраски забора. Далее нужно округлить количество банок в большую сторону, так как часть банки нам никто не продаст и целое количество банок умножить на стоимость одной банки краски, а далее к получившей сумме останется только добавить стоимость доставки заказа.

Вот так легко мы справились с заданием №5! Надеюсь, что вам уже не страшно приступать к этому номеру. Чтобы вы без проблем могли с ним справиться, поделюсь с вами алгоритмом. Он поможет ничего не упустить в ходе решения заданий.

Алгоритм решения задания №5 ОГЭ по математике

1. Внимательно читаем условие. Что дано, что нужно найти?
2. Зачёркиваем все лишние данные, если они есть в таблице.
3. Просчитываем стоимость набора товаров или услуг отдельно для каждого магазина / сервиса.
4. Сравниваем получившиеся варианты по стоимости и выбираем самый дешёвый.
5. В ответ записываем то, что просят. Строго по условию!

Посмотрим еще на два задания. Чтобы вам было интереснее, мы возьмём задачи из двух самых сложных и страшных сюжетов – «План местности» и «Автомобильное колесо».

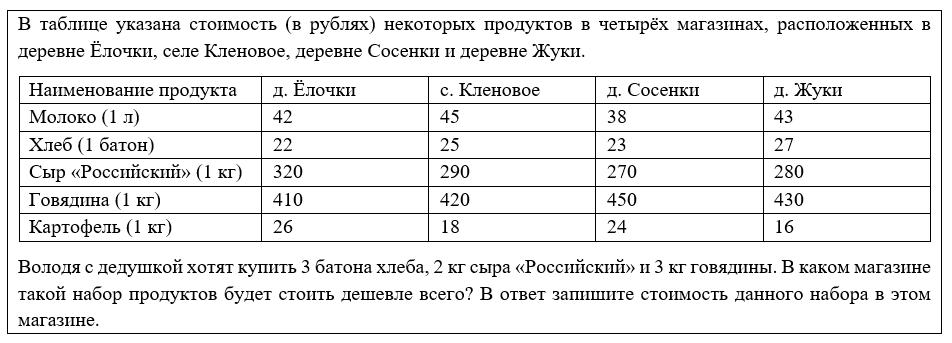
Сначала отработаем алгоритм на задаче из сюжета «План местности».

Решение. В данном прототипе нужно посчитать, сколько денег понадобится заплатить за самый дешёвый набор продуктов. При этом не важно, какими дорогами Володя с дедушкой поедут (просёлочными или асфальтированными), не нужно знать, какой путь самый короткий. Используем наш алгоритм.

Вот нам и покорился неприступный пятый номер, которым известна реальная математика в ОГЭ.

Наконец, рассмотрим пятый номер из сложного сюжета «Автомобильное колесо».

Решение. Видим, что опять нас просят выбрать самый дешёвый вариант. На этот раз меняем резину на колёсах автомобиля. Алгоритм работает, меняется лишь формула подсчёта.

Что нужно запомнить?

1. Пятое задание не страшное, многие прототипы решаются быстро и легко по единому алгоритму
2. Всего существует 7 прототипов задач из модуля ОГЭ «Реальная математика». Найти все эти задания ты можешь на сайте ФИПИ
3. Внимательное прочитай условие. Тогда задание станет намного проще и понятнее.
4. Разбери все прототипы, тогда ты легко получишь все 5 баллов за этот блок!

Вот мы и закончили разбираться с последним заданием из блока «Реальная математика» в ОГЭ. Мы посмотрели только лишь на часть прототипов, поэтому следи за нашим блогом и жди новые статьи. Внимательно читай условие, используй алгоритм, и пусть тебе покорится пятый номер! Если захочешь разобраться с другими заданиями и эффективно подготовиться к ОГЭ по математике, напоминаем про наши онлайн-курсы.

План участка (хозяйственная задача)

Первые пять заданий ОГЭ 2020 по математике объединяет одна картинка, на которой изображен план участка. Под картинкой располагается текст, описывающий расположение объектов на этой картинке.

Для успешного выполнения этих заданий потребуется внимательность, умение логически мыслить, вычислять площадь прямоугольника, и применять теорему Пифагора.

Прочитайте внимательно текст и выполните задания 1-5.

На плане изображено домохозяйство по адресу: с. Авдеево,3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки. Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.

Задание №1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

Таблица соответствия объектов номерам на картинке.

По условию задачи справа от ворот находится баня (6), а слева гараж (7 – по условию). Ещё на участке есть сарай, жилой дом и теплица. На огороде (2 – по условию) стоит теплица (1), рядом с гаражом (7) стоит сарай (4). Яблоневые посадки (5 – по условию) находятся рядом с домом, следовательно дом (3).

Ответ: 3461

Задание №2. Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?

Посмотрим на картинку. По условию задачи одна тротуарная плитка имеет размер 1м×1м и на картинке отмечена серым цветом. Нам нужно сосчитать количество серых плиток на рисунке. Площадку перед гаражом покрывают 4х16=64 плитки, дорожки застелены 26 плитками. Всего плиток 64+26=90 штук. Чтобы понять, сколько упаковок нам нужно купить, разделим общее количество плиток на количество плиток в одной упаковке: 90/4=22,5. В магазине плитка продаётся целыми пачками, поэтому придется брать 23 упаковки, округление с избытком.

Ответ: 23

Задание №3. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.

Сперва посчитаем, сколько тетрадных клеток занимает дом (3). Дом занимает 17 тетрадных клеток. Далее есть три пути решения:

Путь 1 (знаем сторону клетки): На рисунке показано, что сторона одной квадратной клетки составляет 2 м. Значит площадь одной квадратной клетки равна 2×2=4 кв. м. А площадь дома равна 4×17=68 кв. м.

Путь 2 (через площадь плитки): Если бы размер одной клетки не был нам дан, пришлось бы решать задачу другим способом. Одну тетрадную клетку можно застелить четырьмя серыми плитками. Площадь одной плитки составляет 1 кв. м., значит площадь одной тетрадной клетки составляет 4 кв. м. Площадь дома равна 4×17=68 кв. м.

Путь 3 (через площадь сарая): По условию задачи площадь гаража (7) равна 32 кв. м. Гараж занимает 8 тетрадных клеток, следовательно, площадь одной тетрадной клетки равна 32/8=4 кв. м. Тогда площадь дома равна 4×17=68 кв. м.

Все три пути решения привели нас к одному и тому же ответу, и это однозначно успех .

Ответ: 68

Задание №4. Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.

Посмотрим на картинку.
Проведём красным цветом кратчайший отрезок, соединяющий дом (3) и сарай (7). Этот орезок является гипотенузой в прямоугольном треугольнике с катемтами 3 и 4 клетки. Длина стороны одной клетки по условию 2м, значит один катет 6м, а другой 8м. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит:

x = ± 10 = [ − 10 не подходит 10 подходит

Ответ: 10

Задание №5. Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице. Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?

Цены на оборудование и стоимость его установки.

Вычислим, сколько денег переплатил хозяин, установив газовое оборудование:

24000 – 20000 + 18280 – 15000 = 4000 + 3280 = 7280

Хозяин переплатил 7280 рублей, установив газовое оборудование. Вычислим, сколько экономит хозяин в час, используя газовое оборудование вместо электрического отопления:

5 , 6 ⋅ 3 , 8 – 1 , 2 ⋅ 5 , 6 = 5 , 6 ⋅ ( 3 , 8 – 1 , 2 ) = 5 , 6 ⋅ 2 , 6 = 14 , 56

Каждый час работы газового оборудования хозяин экономит 14,56 рубля. Пусть генератор работал непрерывно x часов. Тогда:

x ⋅ 14 , 56 = 7280

x = 7280 14 , 56 = 500

За 500 часов непрерывной работы экономия от использования газового оборудования покроет переплату за его установку.

ОГЭ по математике 2020: задача про печку

Разбор задачи в диагностической работе СтатГрад от 5 марта 2020 года

В 2019-2020 учебном году выпускники 9 классов будут сдавать ОГЭ по обновлённым заданиям. Представляем вам вариант тренировочной работы по математике в формате ОГЭ от СтатГрада (5 марта 2020 года). Рассказываем, как работать с новыми заданиями про печку.

Хозяин дачного участка строит баню с парным отделением. Размеры парного отделения: длина — 3,9 м, ширина — 2,1 м, высота — 2 м. Для разогрева парного помещения можно использовать электрическую или дровяную печь. Три возможных варианта даны в таблице.

Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6 200 руб. Кроме того, хозяин подсчитал, что за год электрическая печь израсходует 2 300 киловатт-часов электроэнергии по 3,5 руб. за 1 киловатт-час, а дровяная печь за год израсходует 1,6 куб. м дров, которые обойдутся по 1 700 руб. за 1 куб. м.

Задание 1. Найдите объём парного отделения строящейся бани (в куб. м).

Решение: парное отделение, объём которого надо найти, представляет собой прямоугольник, значит, его объём — это произведение всех его измерений.

3,9 х 2,1 х 2 = 16,38

Задание 2. На сколько рублей дровяная печь, подходящая по отапливаемому объёму парного отделения, обойдётся дешевле электрической с учётом установки?

Решение : электрическая печь требует дополнительных расходов на кабель — 6 200 руб.

(16 000 + 6 200) — 20 500 = 22 200 — 20 500 = 1 700

Задание 3. На сколько рублей эксплуатация дровяной печи обойдётся дешевле эксплуатации электрической в течение года?

Решение : электрическая печь в год потребляет 2 300 киловатт-часов электроэнергии по 3,5 руб. за один киловатт-час, а дровяная печь — 1,6 куб. м дров, которые обойдутся по 1 700 руб. за 1 куб. м.

2 300 х 35 — 1 700 х 1,6 = 8 050 — 2 720 = 5 330

Задание 4. Доставка печи из магазина до участка стоит 700 рублей. При покупке печи ценой выше 19 000 рублей магазин предлагает скидку 5 % на товар и 20 % на доставку. Сколько будет стоить покупка печи Б вместе с доставкой на этих условиях?

Решение: 20 500 х 0,95 + 700 х 0,80 = 19 475 + 560 = 20 035

Задание 5. Хозяин выбрал дровяную печь. Чертёж печи показан на рисунке.

Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности. Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус в сантиметрах.

Решение: необходимо найти радиус закругления, для этого проведем ещё несколько радиусов, теперь мы можем узнать хорду.

Длина хорды равна 36. Мы знаем разницу между длиной радиуса и расстоянием от центра закругления до хорды — это 8 (61-53=8). Расстояние от центра закругления до нашей хорды — это Х — 8. За Х мы берём сам радиус.

Теперь у нас есть треугольник, для которого мы можем составить теорему Пифагора.

Хотите видеть в ленте своих соцсетей ещё больше наших статей про ОГЭ? Добавляйтесь в друзья в наших пабликах: