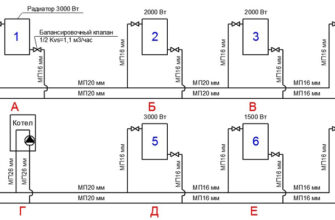
Что называют местными сопротивлениями элементов систем отопления

Ниже рассмотрим задачу

КМС – это значение, характеризующее гидравлическое сопротивление. Но этим значением является коэффициент. Коэффициент указан в формуле. Формулу рассмотрим ниже.

КМС – Коэффициент местного сопротивления

Этот коэффициент присваивается элементами систем водоснабжения и отопления, в которых происходит гидравлическое сопротивление за счет деформации потока воды или теплоносителя. Там где происходит деформация потока жидкости — называют местными сопротивлениями.

Также местные сопротивления наблюдаются в различных клапанах.

Элементы, которым присваивается КМС

Отвод; Тройник; Термостатический клапан; Трехходовой клапан; Различные регулировочный клапана и тому подобное.

Местные гидравлические сопротивления можно выразить в пропускной способности Kvs.

Связь гидравлического сопротивления, диаметра и КМС

P – Гидравлическое сопротивление, м.в.ст. (метр водяного столба) Значение потерь напора V – Скорость движения воды или теплоносителя, метр/сек g – Ускорение свободного падения, 9,8 метр/сек 2

Таблица КМС различных элементов

Если КМС привязывается к диаметру, то это означает что КМС для клапана любого диаметра остается одинаковым. Потому что гидравлическое сопротивление находится исходя из скорости движения жидкости.

Найти гидравлическое сопротивление (потерю напора), фильтра грязевика 1” при расходе 40 л./мин.

Гидравлическое сопротивление = потеря напора = значение манометр 1 — значение манометра 2.

Внутренний проходной диаметр 1” элемента равен 25 мм

Таблица других элементов

Находим скорость воды

Q = 40л/мин = 0,00066666 м3/час

D = 25мм = 0,025 метров

Находим потерю напора

Ответ: Потеря напора составляет 0,94 м.в.ст. = 0,092 Bar = (манометр 1 – манометр 2)

1 Bar = 10,1972 м.в.ст. (метр водяного столба)

Гидравлическое сопротивление

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:

Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.

Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.

Содержание статьи

Коэффициент гидравлического сопротивления

Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:

где ρ — плотность среды, g — ускорение свободного падения.

В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:
Поворотов
Диафрагм
Задвижек
Вентилей
Кранов
Различных ответвлений и тому подобного

На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.

Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.

где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).

Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.

Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.

В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.

Местные гидравлические сопротивления

Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.

Гидравлические потери на внезапное сужение трубы

Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.

Значение коэффициента ξ_{вн. суж} от значения отношения (F₂/F₁)) можно найти в соответствующем справочнике по гидравлике.

Гидравлические потери при изменении направления трубопровода под некоторым углом

В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле

ξ _{поворот} = 0,946sin(α/2) + 2.047sin(α/2) 2

где α – угол поворота трубопровода.

Местные гидравлические сопротивления при входе в трубу

В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.

Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:

ξ_вх = 0,505 + 0,303sin α + 0,223 sin α 2

Местные гидравлические сопротивления задвижки

На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.

Гидравлическое сопротивление полностью открытой запорной арматуры равно

ξ_{вентиля} = от 2,9 до 4,5

Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.

Гидравлические потери диафрагмы

Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:
режима движения жидкости
отношения диаметров отверстия диафрагмы и трубы
конструктивных особенностей диафрагмы.

Для диафрагмы с острыми краями:

Местные гидравлические сопротивления при входе струи под уровень жидкости

Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.

Видео о гидравлическом сопротивлении

На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)

Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.

Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.

КОЭФФИЦИЕНТЫ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ СИСТЕМ ТЕПЛОСНАБЖЕНИЯ И ОТОПЛЕНИЯ.

Все гидравлические потер и энергии делятся на два типа: потери на трение по длине трубопроводов и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.

Трубопроводы, по которым течет жидкость, часто имеют в своем составе всевозможные сужения, расширения, повороты и дросселирующие устройства, называемые простейшими местными гидравлическими сопротивлениями. В практических расчетах трубопроводов обычно руководствуются следующим правилом. Если длина трубопроводов значительна, а местных сопротивлений немного, то потери напора в местных сопротивлениях не учитывают, но для компенсации этих потерь длину трубопровода при расчете увеличивают на 5 — 10%.
Если трубопроводы короткие, а местных сопротивлений много, то потери напора в них учитывают самым тщательным образом.

Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.

1. Внезапное расширение русла.

Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.

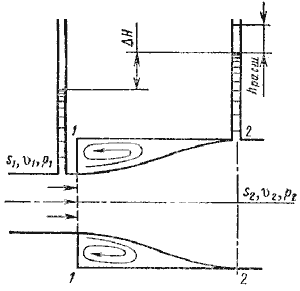
Рисунок 24 – Внезапное расширение трубы

При внезапном расширении русла (трубы) (рисунок 19) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 — в плоскости расширения трубы и 2-2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на h_расш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:

(22)

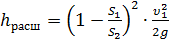
где S1, S2 — площадь поперечных сечений 1-1 и 2-2.

Это выражение является следствием теоремыБорда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей

(23)

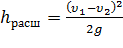
Выражение (1 – S₁/S₂ ) 2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

(24)

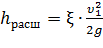
2. Постепенное расширение русла.

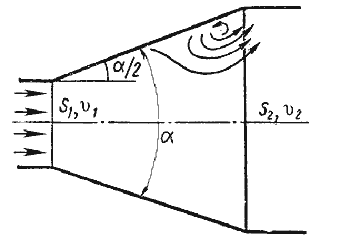
Расширяющаяся труба называется диффузором. Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Рисунок 25 – Постепенное расширение трубы

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

(25)

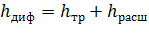
где h_тр и h_расш — потери напора на трение и расширение (вихреобразование).

(26)

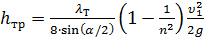
где n = S₂/S₁ = ( r₂/r₁ ) 2 — степень расширения диффузора. Потеря напора на расширение h_расш имеет ту же самую природу, что и при внезапном расширении русла

(27)

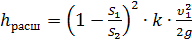
где k — коэффициент смягчения, при α= 5…20°, k = sinα.

Учитывая это полную потерю напора можно переписать в виде:

(28)

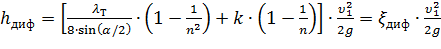
откуда коэффициент сопротивления диффузора можно выразить формулой

(29)

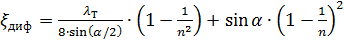
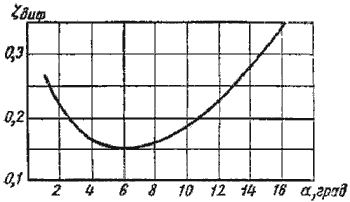
Рисунок 26 – Зависимость ζ_диф от угла

Функция ζ = f(α) имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:

(30)

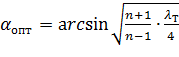
При подстановке в эту формулу λ_Т =0,015…0,025 и n = 2…4 получим α_опт = 6 (рисунок 26).

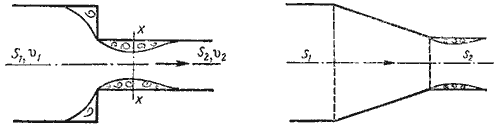
3. Внезапное сужение русла.

В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока.

Рисунок 27 – Внезапное сужение трубы

Рисунок 28 – Конфузор

Полная потеря напора определится по формуле:

(31)

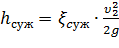
где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:

(32)

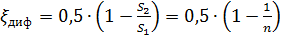
в которой n = S₁/S₂ — степень сужения.

При выходе трубы из резервуара больших размеров, когда можно считать, что S₂/S₁ = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζ_суж = 0,5.

4. Постепенное сужение русла.

Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рисунок 27). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение

(33)

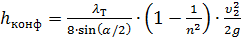
где коэффициент сопротивления конфузора определяется по формуле

(34)

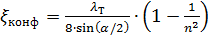
в которой n = S₁/S₂ — степень сужения.

Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рисунок 29).

Рисунок 29 – Сопло

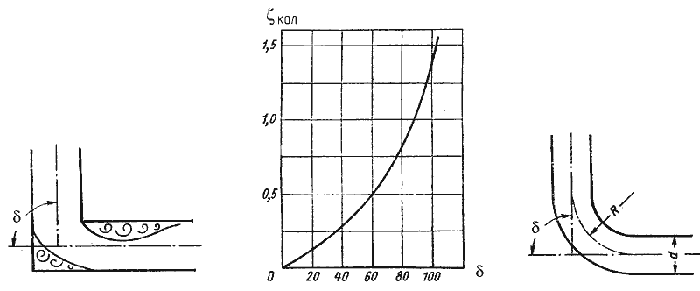
5. Внезапный поворот трубы (колено).

Данный вид местного сопротивления (рисунок 30) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

(35)

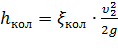
где ζ_кол — коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рисунок 31).

Рисунок 30 — Внезапный поворот трубы (колено).

Рисунок 31 — Зависимости ζкол от угла δ

Рисунок 32 – Отвод

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R/d рисунок 32). Коэффициент сопротивления отвода ζ_отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

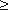
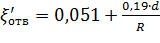
Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:

(36)

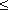
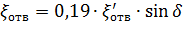
Для углов δ 70° коэффициент сопротивления

(37)

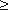
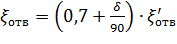
а при δ 100°

(38)

Потеря напора в колене определится как

(39)

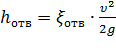
Иногда при расчете систем трубопроводов с большим числом местных сопротивлений потери напора в них вычисляют по их эквивалентным длинам. Длиной, эквивалентной данному местному сопротивлению, считается такая длина прямой трубы (того же диаметра, как и номинальный диаметр рассчитываемого трубопровода), на протяжении которой гидравлические потери равны потерям в данном сопротивлении. В результате такой замены все местные сопротивления в системе устраняются, длины труб соответственно увеличиваются и далее рассчитывается только прямолинейный трубопровод.

Пусть, например, надо заменить местное сопротивление С коэффициентом ζ трубой эквивалентной длины lэ диаметром d.
Значение эквивалентных длин для каждого значения ζ берется из таблиц соответствующих справочников. Таблицы КМС приведены в приложениях.

Для расчета характеристики участка составляем таблицу коэффициентов местного сопротивления циркуляционного кольца (таблица 22)

Таблица 22 – Ведомость коэффициентов местных сопротивлений циркуляционного кольца