Практическое использование реактивной энергии
Вот цитата из учебника «Электротехника с основами электроники» авторов Зороховича и Калинина для техникумов. В параграфе «Активная и реактивная мощности» читаем на стр. 121:
«…только активная мощность может обеспечить в приёмнике преобразование электрической энергии в другие виды энергии».
«…Реактивная мощность никакой полезной работы не создаёт, так как её среднее значение в течение одного периода равно нулю…».
Цель опыта – это практическая проверка данной цитаты из учебника.
Вступление
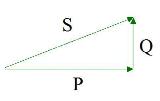
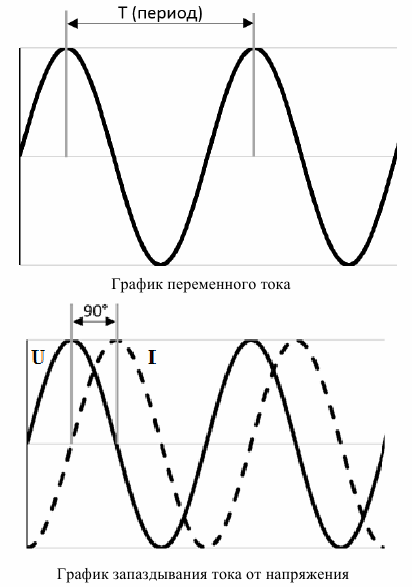
В электрической сети совершаются гармонические и синфазные (!) колебания тока и напряжения с частотой 50 Гц. При этом ток и напряжение совпадают по фазе. В этом может убедиться каждый желающий, подключив через шунт 0,5 Ом к сети активную нагрузку (например, лампу накаливания) и подключив к ним осциллограф (соблюдая технику безопасности). Для этой цели лучше использовать сетевой разделительный трансформатор 220 на 220 В. Вначале нужно найти и пометить в розетке фазный и нулевой провод. Как на активной нагрузке будут выглядеть вместе колебания тока и напряжения, показано на Рис.1
Но если ко вторичной обмотке трансформатора подключить реактивную нагрузку в виде конденсатора, то колебания тока и напряжения будут сдвинуты относительно друг друга по фазе на 90º. Всё это можно проверить тем же способом, что и с активной нагрузкой, подключив осциллограф к шунту и к конденсатору. Осциллограммы тока и напряжения для этого случая приведены ниже на Рис.2
Подключение в качестве реактивной нагрузки катушки индуктивности приведёт к обратному явлению. В качестве индуктивности можно использовать первичную обмотку любого силового трансформатора. В цепи такой обмотки колебания тока по фазе будут отставать от колебаний напряжения на 90º.
Если у этого сетевого трансформатора есть вторичная обмотка (хорошо, если она будет на 12÷20 Вольт), то мы всегда можем собрать колебательный контур, состоящий из вторичной обмотки данного сетевого трансформатора и конденсатора, чтобы резонансная частота полученного колебательного контура совпала с частотой колебаний в сети (50 Гц).
Настройку колебательного контура лучше выполнить практически, а не по расчётам, чтобы убедиться в том, что данный колебательный контур действительно находится в резонансе с колебаниями сети. Для этого понадобится низкоомный амперметр. Если в хозяйстве нет амперметра на 20÷100 ампер, то можно в разрыв колебательного контура включить шунт сопротивлением приблизительно 0,05 Ом, подключить к нему осциллограф и установить величину реактивного тока в этом колебательном контуре. Значение реактивного тока в колебательном контуре может достигать десятков ампер. Затем, подключая параллельно к основному конденсатору любой конденсатор небольшой емкости, надо наблюдать, что происходит с амплитудой колебания тока в контуре. Если ток продолжает возрастать, то добавляем следующий конденсатор, пока ток в контуре не начнёт убывать. После чего удаляем этот последний конденсатор, измеряем общую ёмкость всех конденсаторов и заменяем их одним или двумя конденсаторами с мощными выводами, рассчитанными на большой реактивный ток.
Напомню о технике безопасности при работе с конденсаторами. Имея дело с полярными конденсаторами, помните, что их нельзя поодиночке включать в цепь переменного тока, а только парами, при условии, что они соединены последовательно и встречно. Это означает, что плюсовой вывод одного конденсатора нужно подключать к плюсовому выводу другого конденсатора или наоборот – соединять их вместе минусовыми выводами. Такие пары конденсаторов уже можно включать в цепь переменного тока, важно лишь, чтобы рабочее напряжение не превышало их паспортное значение.
Второй важный момент заключается в том, что надо следить за нагревом конденсаторов. Если нет возможности приобрести конденсаторы, рассчитанные на большую реактивную мощность (измеряемую в кВАр-ах), то допускается подключение конденсаторов, не рассчитанных на большой реактивный ток, но только на короткое время, при условии, что мы будем следить за их тепловым режимом и не допускать перегрева конденсаторов, что чревато их взрывом. Допускается нагрев до 60÷85º и более, в зависимости от типа конкретного конденсатора.
Итак, при подключенном к вторичной обмотке нашего сетевого трансформатора реактивном элементе — конденсаторе, ток и напряжение в колебательном контуре окажутся сдвинутыми по фазе почти на 900, при условии, конечно, что сечение провода вторичной обмотки и реактивная мощность конденсатора окажутся приличными. Интересно отметить одну важную деталь. Наш трансформатор не только не заметит подключение такого настроенного конденсатора, но и ток его потребления от сети значительно снизится. Об этом я скажу в конце этой работы.
Но, если вместо конденсатора к вторичной обмотке этого же трансформатора подключить активную нагрузку (например, лампочку накаливания), то напряжение и ток снова будут стремиться стать синфазными (сдвиг фаз между их колебаниями будет стремиться к нулю). При этом ток потребления трансформатора немедленно повысится, в соответствии с величиной мощности подключенной активной нагрузки.
При подключении активной нагрузки к вторичной обмотке, сердечник трансформатора намагничивается пропорционально величине тока в нагрузке, а при коротком замыкании вторичной обмотки он может войти в насыщение. При насыщении сердечника трансформатора его магнитные свойства резко снижаются, в результате индуктивность первичной обмотки резко снижается, что сопровождается резким возрастанием тока в первичной обмотке трансформатора и, соответственно, возрастает потребляемая трансформатором от сети мощность. Но реактивные элементы (катушки и конденсаторы), подключаемые параллельно вторичной обмотке трансформатора и настроенные в резонанс с колебаниями в сети, такого эффекта не вызывают (!), несмотря на то, что в цепи колебательного контура вторичной обмотки реактивные токи будут достигать десятков ампер! Возникает интересный вопрос: а можно ли как-то использовать свободные реактивные мощности, достигающие в колебательных контурах огромных значений?
Я не стану рассматривать здесь все виды нагрузок. Кому надо, сами найдёте нужную вам информацию в книгах или в Интернете. А здесь пойдёт речь о возможности аккумулирования и использовании реактивной энергии, свободно гуляющей по колебательному контуру.
А что если в момент, когда напряжение во вторичной обмотке равно нулю, подключить к ней через диод конденсатор и в течение первой четверти периода его заряжать, при условии, что данный конденсатор и вторичная обмотка трансформатора составляют колебательный контур с резонансной частотой 50 Гц? Следовательно, зарядить конденсатор нужно успеть за 20/4=5ms, то есть за первую четверть одного периода колебания (50 Гц).
Если конденсатор зарядится, то, когда напряжение в контуре достигнет максимального значения, нужно отключить конденсатор от вторичной обмотки, так как он больше не сможет зарядиться, а затем разрядить его на активную нагрузку в течение второй четверти периода длительностью 5 ms.
Если этот опыт удастся, то мы можем надеяться, что когда-нибудь сможем научиться использовать свободно гуляющую реактивную мощность в практических целях.
Что такое реактивная мощность и как с ней бороться
Реактивная мощность определяет периодический обмен электрической энергией между источником и электроприемником с двойной частотой по отношению к частоте переменного тока без преобразования ее в другой вид энергии и может рассматриваться как характеристика скорости обмена электроэнергией между источником и магнитным полем электроприемника.
Суммарная энергия, связанная с существованием этой составляющей мгновенной мощности, равна нулю. Ее появление, очевидно, связано с наличием в системе производства, передачи и распределения электроэнергии элементов, в которых возможно периодическое накопление и последующий возврат определенного количества энергии. В противном случае обмен электрической энергией между источником и электроприемником был бы невозможен.
Физика процесса и практика применения установок компенсации реактивной мощности
Чтобы разобраться с понятием реактивной мощности, вспомним сначала, что такое электрическая мощность. Электрическая мощность – это физическая величина, характеризующая скорость генерации, передачи или потребления электрической энергии в единицу времени.
Чем больше мощность, тем большую работу может совершить электроустановка в единицу времени. Измеряется мощность в ваттах (произведение Вольт х Ампер). Мгновенная мощность – это произведение мгновенных значений напряжения и силы тока на каком-то участке электрической цепи.
Физика процесса
В цепях постоянного тока значение мгновенной и средней мощности за какой-то промежуток времени совпадают, а понятие реактивной мощности отсутствует. В цепях переменного тока так происходит только в том случае, если нагрузка чисто активная. Это, например, электронагреватель или лампа накаливания. При такой нагрузке в цепи переменного тока фаза напряжения и фаза тока совпадают и вся мощность передается в нагрузку.
Если нагрузка индуктивная (трансформаторы, электродвигатели), то ток отстает по фазе от напряжения, если нагрузка емкостная (различные электронные устройства), то ток по фазе опережает напряжение. Поскольку ток и напряжение не совпадают по фазе (реактивная нагрузка), то в нагрузку (потребителю) передается только часть мощности (полной мощности), которая могла бы быть передана в нагрузку, если бы сдвиг фаз был равен нулю (активная нагрузка).
Активная и реактивная мощности
Часть полной мощности, которую удалось передать в нагрузку за период переменного тока, называется активной мощностью. Она равна произведению действующих значений тока и напряжения на косинус угла сдвига фаз между ними (cos φ ).
Мощность, которая не была передана в нагрузку, а привела к потерям на нагрев и излучение, называется реактивной мощностью. Она равна произведению действующих значений тока и напряжения на синус угла сдвига фаз между ними (sin φ).
Таким образом, реактивная мощность является величиной характеризующей нагрузку. Она измеряется в вольт амперах реактивных (вар, var). На практике чаще встречается понятие косинус фи, как величины характеризующей качество электроустановке с точки зрения экономии электроэнергии.
Действительно, чем выше cos φ, тем больше энергии, подаваемой от источника, попадает в нагрузку. Значит можно использовать менее мощный источник и меньше энергии пропадает зря.
Реактивная мощность может рассматриваться как характеристика скорости обмена электрической энергией между источником и магнитным полем электроприемника. В отличие от активной мощности реактивная мощность не выполняет непосредственно полезной работы, она служит для создания переменных магнитных полей в индуктивных электроприемниках (например, в асинхронных двигателях, силовых трансформаторах и др.), непрерывно циркулируя между источником и потребляющими ее электроприемниками.
Реактивная мощность бытовых потребителей
Итак, потребители переменного тока имеют такой параметр, как коэффициент мощности cosφ.
На графике ток сдвинут на 90° (для наглядности), то есть на четверть периода. Например, электрооборудование имеет cosφ = 0,8, что соответствует углу arccos 0,8 ≈ 36.8°. Этот сдвиг происходит из-за наличия в потребителе электроэнергии нелинейных компонентов – ёмкостей и индуктивностей (например, обмотки электродвигателей, трансформаторов и электромагнитов).
Для дальнейшего понимания происходящего требуется учет того факта, что, чем выше коэффициент мощности (максимум 1), тем более эффективно потребитель использует получаемую из сети электроэнергию (то есть большее количество энергии преобразуется в полезную работу) – такую нагрузку называют резистивной.
При резистивной нагрузке ток в цепи совпадает с напряжением. А при низком коэффициенте мощности нагрузку называют реактивной, то есть часть потребляемой мощности не совершает полезной работы.
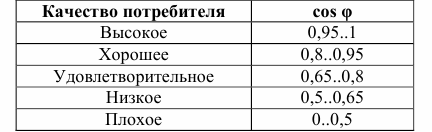
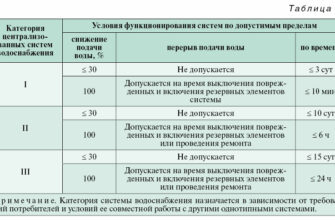
Таблица ниже демонстрирует классификацию потребителей по коэффициенту мощности.
Классификация потребителей переменного тока
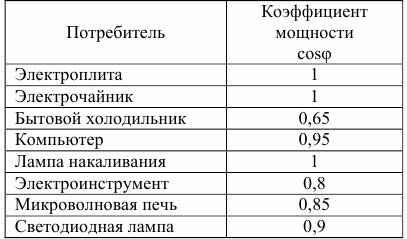
Следующая таблица демонстрирует коэффициент мощности распространённых в быту потребителей электроэнергии.
Коэффициент мощности бытовых электроприборов
Юмор электрика
Что такое реактивная мощность? Все очень просто!
Способы компенсации реактивной мощности
Из сказанного выше вытекает, если нагрузка индуктивная, то следует компенсировать ее с помощью емкостей (конденсаторов) и наоборот емкостную нагрузку компенсируют с помощью индуктивностей (дросселей и реакторов). Это помогает увеличить косинус фи (cos φ) до приемлемых значений 0.7-0.9. Этот процесс называется компенсацией реактивной мощности.
Экономический эффект от компенсации реактивной мощности
Экономический эффект от внедрения установок компенсации реактивной мощности может быть очень большим. По статистике он составляет от 12 до 50% от оплаты электроэнергии в различных регионах России. Установка компенсации реактивной мощности окупается не более чем за год.
Для проектируемых объектов внедрение конденсаторной установки на этапе разработки позволяет экономить на стоимости кабельных линий за счет снижения их сечения. Автоматическая конденсаторная установка, например, может поднять cos φ с 0.6 до 0.97.
Выводы
Итак, установки по компенсации реактивной мощности приносят ощутимые финансовые выгоды. Они также позволяют дольше сохранять оборудование в рабочем состоянии.
Вот несколько причин, по которым это происходит.
1. Уменьшение нагрузки на силовые трансформаторы, увеличение в связи с этим срока их службы.
2. Уменьшение нагрузки на провода и кабели, возможность использования кабелей меньшего сечения.
3. Улучшение качества электроэнергии у электроприемников.
4. Ликвидация возможности штрафов за снижение cos φ.
5. Уменьшение уровня высших гармоник в сети.
6. Снижение уровня потребления электроэнергии.
