Коэффициент сопротивления трубы отопления

Расчет гидравлического сопротивления в системе отопления.

Ниже будут реальные задачи.

Вы, конечно, можете воспользоваться специальными программами, для этого, но пользоваться программами весьма затруднительно, если вы не знаете основ гидравлики. Что касается некоторых программ, то в них не разжевываются формулы, по которым происходит гидравлический расчет. В некоторых программах не описываются некоторые особенности по разветвлению трубопроводов, и нахождению сопротивления в сложных схемах. И весьма затруднительно считать, это требует дополнительного образования и научно-технического подхода.

В этой статье я раскрываю для Вас абсолютный расчет (алгоритм) по нахождению гидравлического сопротивления.

Существуют местные гидравлические сопротивления, которые создают различные элементы систем, например: Шаровый кран, различные повороты, заужения или расширения, трайники и тому подобное. Казалось бы, с поворотами и сужениями понятно, а расширения в трубах тоже создают гидравлические сопротивления.

Протяженность прямой трубы тоже создает сопротивление движению. Вроде прямая труба без сужений, а все равно создает сопротивление движению. И чем длиннее труба, тем больше сопротивление в ней.

Эти сопротивления, хоть и отличаются, но для системы отопления они просто создают сопротивление движению, а вот формулы по нахождению этого сопротивления отличаются между собой.

Для системы отопления не важно, какое это сопротивление местное или по длине трубопровода. Это сопротивление одинаково действует на движение воды в трубопроводе.

Сопротивление будем измерять в метрах водяного столба. Также сопротивление можно обзывать как потеря напора в трубопроводе. Но только однозначно это сопротивление измеряется в метрах водяного столба, либо переводится в другие единицы измерения, например: Bar, атмосфера, Па (Паскаль) и тому подобное.

Что такое сопротивление в трубопроводе?

Чтобы понять это рассмотрим участок трубы.

Манометры, установленные на подающей и обратной ветке трубопроводов, показывают давление на подающей трубе и на обратной трубе. Разница между манометрами показывает перепад давления между двумя точками до насоса и после насоса.

Для примера предположим, что на подающем трубопроводе (справа) стрелка манометра указывает на 2,3 Bar, а на обратном трубопроводе (слева) стрелка манометра показывает 0,9 Bar. Это означает, что перепад давления составляет:

Величину Bar переводим в метры водяного столба, оно составляет 14 метров.

Очень важно понять, что перепад давления, напор насоса и сопротивление в трубе — это величины, которые измеряются давлением (Метрами водяного столба, Bar, Па и т.д.)

В данном случае, как указано на изображение с манометрами, разница на манометрах показывает не только перепад давления между двумя точками, но и напор насоса в данном конкретном времени, а также показывает сопротивление в трубопроводе со всеми элементами, встречающимися на пути трубопровода.

Другими словами, сопротивление системы отопления это и есть перепад давления в пути трубопровода. Насос создает этот перепад давления.

Устанавливая манометры на две разные точки, можно будет находить потери напора в разных точках трубопровода, на которые Вы установите манометры.

На стадии проектирования нет возможности создавать похожие развязки и устанавливать на них манометры, а если имеется такая возможность, то она очень затратная. Для точного расчета перепада давления манометры должны быть установлены на одинаковые трубопроводы, то есть исключить в них разность диаметров и исключить разность направление движения жидкости. Также манометры не должны быть на разных высотах от уровня горизонта.

Ученые приготовили для нас полезные формулы, которые помогают находить потери напора теоретическим способом, не прибегая к практическим проверкам.

Разберем сопротивление водяного теплого пола. Смотри изображение.

Труба металлопластиковая 16мм, внутренний диаметр 12мм. длина трубы 40 м. По условию обогрева, расход в контуре должен быть 1,6 л/мин Поворотов 90 градусов соответствует: 30 шт. Температура теплоносителя (воды): 40 градусов Цельсия.

Для решения данной задачи были использованы следующие материалы:

Первым делом находим скорость течения в трубе.

Q= 1,6 л/мин = 0,096 м 3 /ч = 0,000026666 м 3 /сек.

V = (4•0,000026666)/(3,14•0,012•0,012)=0,24 м/с

Находим число Рейнольдса

ν=0,65•10 -6 =0,00000065. Взято из таблицы. Для воды при температуре 40°С.

Δэ=0,01мм=0,00001м. Взято из таблицы, для металлопластиковой трубы.

Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.

У меня попадает на первую область при условии

4000 0,25 = 0,3164/4430 0,25 = 0,039

Далее завершаем формулой:

h=λ•(L•V 2 )/(D•2•g)= 0,039•(40•0,24•0,24)/(0,012•2•9,81)= 0,38 м.

Находим сопротивление на поворотах

h=ζ•(V 2 )/2•9,81=(0,31•0,24 2 )/( 2•9,81)= 0,00091 м.

Данное число умножаем на количество поворотов 90 градусов

В итоге полное сопротивление уложенной трубы составляет: 0,38+0,0273=0,4 м.

Теория о местном сопротивление

Хочу подметить процесс вычисления местных сопротивлений на поворотах и различных расширений и сужений в трубопроводе.

Потеря напора на местном сопротивление находится по этой формуле:

h-потеря напора здесь она измеряется в метрах. ζ-Это коэффициент сопротивления, он будет находиться дополнительными формулами, о которых напишу ниже. V — скорость потока жидкости. Измеряется [Метр/секунда]. g — ускорение свободного падения равен 9,81 м/с 2

В этой формуле меняется только коэффициент местного сопротивления, коэффициент местного сопротивления для каждого элемента свой.

Подробнее о нахождение коэффициента

Обычный отвод в 90 градусов.

Коэффициент местного сопротивления составляет примерно единице.

Формула для других углов:

Постепенный или плавный поворот трубы

Постепенный поворот трубы (отвод или закруглённое колено) значительно уменьшает гидравлическое сопротивление. Величина потерь существенно зависит от отношения R/d и угла α.

Коэффициент местного сопротивления для плавного поворота можно определить по экспериментальным формулам. Для поворота под углом 90° и R/d>1 он равен:

для угла поворота более 100°

Для угла поворота менее 70°

Для теплого пола, поворот трубы в 90° составляет: 0,31-0,51

где n степень сужения трубы.

ω1, ω2 — сечение внутреннего прохода трубы.

В формулу вставляется скорость течения в трубе с малым диаметром.

В формулу вставляется скорость течения в трубе с малым диаметром.

Также существуют и плавные расширения и сужения, но в них сопротивление потоку уже значительно ниже.

Внезапное расширение и сужение встречается очень часто, например, при входе в радиатор получается внезапное расширение, а при уходе жидкости из радиатора внезапное сужение. Также внезапное расширение и сужение наблюдается в гидрострелках и коллекторах.

Более детально о разветвлениях поговорим в других статьях.

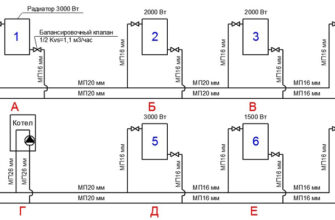
Находим сопротивление для радиаторной системы отопления. Смотри изображение.

Труба металлопластиковая 16мм, внутренний диаметр 12мм. Длина трубы 5 м. По условию обогрева, расход в контуре радиатора должен быть 2 л/мин Плавных поворотов 90 градусов соответствует: 2 шт. Отводов 90 градусов: 2шт. Внезапное расширение на входе в радиатор: 1шт. Внезапное сужение на выходе из радиатора: 1шт. Температура теплоносителя (воды): 60 градусов Цельсия.

Для начала посчитаем сопротивление по длине трубопровода.

Первым делом находим скорость течения в трубе.

Q= 2 л/мин = 0,096 м 3 /ч = 0,000033333 м 3 /сек.

V = (4•0,000033333)/(3,14•0,012•0,012)=0,29 м/с

Находим число Рейнольдса

ν=0,65•10 -6 =0,000000475. Взято из таблицы. Для воды при температуре 60°С.

Δэ=0,01мм=0,00001м. Взято из таблицы, для металлопластиковой трубы.

Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения. У меня попадает на первую область при условии

4000 0,25 = 0,3164/7326 0,25 = 0,034

Далее завершаем формулой:

h=λ•(L•V 2 )/(D•2•g)= 0,034•(5•0,29•0,29)/(0,012•2•9,81)= 0,06 м.

Находим сопротивление на плавном повороте

h=ζ•(V 2 )/2•9,81=(0,31•0,292)/( 2•9,81)= 0,0013 м.

Данное число умножаем на количество поворотов 90 градусов

Находим сопротивление на коленном (прямом 90°) повороте

Там, где имеется сужение и расширение — это тоже будет являться гидравлическим сопротивлением. Я не стану считать сужение и расширение на металлопластиковых фитингах, так как далее мы все равно затронем эту тему. Потом сами посчитаете.

h=ζ•(V 2 )/2•9,81=(2•0,292)/( 2•9,81)= 0,0086 м.

Данное число умножаем на количество поворотов 90 градусов

Находим сопротивление на входе в радиатор.

Вход в радиатор — это ни что иное как расширение трубопровода, поэтому коэффициент местного сопротивления будем находить для трубы идущий на резкое расширение.

Минимальный диаметр примем за 15мм, а максимальный диаметр у радиатора примем за 25мм.

Находим площадь сечения двух разных диаметров:

ω₁ = π • D 2 /4 = 3.14 • 15 2 / 4 = 177 мм 2

ω₂ = π • D 2 /4 = 3.14 • 25 2 / 4 = 491 мм 2

h=ζ•(V 2 )/2•9,81=(0,41•0,19 2 )/( 2•9,81)= 0,00075 м.

Находим сопротивление на выходе из радиатора.

Выход из радиатора — это ни что иное как сужение трубопровода, поэтому коэффициент местного сопротивления будем находить для трубы идущий на резкое сужение.

Площади уже известны

ω₂ = π • D 2 /4 = 3.14 • 15 2 / 4 = 177 мм 2

ω₁ = π • D 2 /4 = 3.14 • 25 2 / 4 = 491 мм 2

h=ζ•(V 2 )/2•9,81=(0,32•0,19 2 )/( 2•9,81)= 0,00059 м.

Далее все потери складываются, если эти потери идут последовательно друг для друга.

Чтобы в ручную не считать всю математику я приготовил специальную программу:

КОЭФФИЦИЕНТЫ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ СИСТЕМ ТЕПЛОСНАБЖЕНИЯ И ОТОПЛЕНИЯ.

Все гидравлические потер и энергии делятся на два типа: потери на трение по длине трубопроводов и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.

Трубопроводы, по которым течет жидкость, часто имеют в своем составе всевозможные сужения, расширения, повороты и дросселирующие устройства, называемые простейшими местными гидравлическими сопротивлениями. В практических расчетах трубопроводов обычно руководствуются следующим правилом. Если длина трубопроводов значительна, а местных сопротивлений немного, то потери напора в местных сопротивлениях не учитывают, но для компенсации этих потерь длину трубопровода при расчете увеличивают на 5 — 10%.
Если трубопроводы короткие, а местных сопротивлений много, то потери напора в них учитывают самым тщательным образом.

Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.

1. Внезапное расширение русла.

Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.

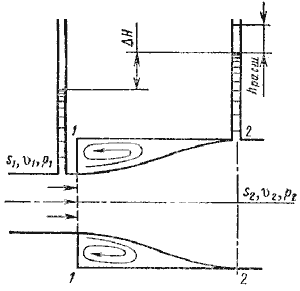
Рисунок 24 – Внезапное расширение трубы

При внезапном расширении русла (трубы) (рисунок 19) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 — в плоскости расширения трубы и 2-2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на h_расш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:

(22)

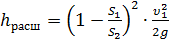
где S1, S2 — площадь поперечных сечений 1-1 и 2-2.

Это выражение является следствием теоремыБорда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей

(23)

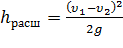
Выражение (1 – S₁/S₂ ) 2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

(24)

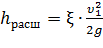
2. Постепенное расширение русла.

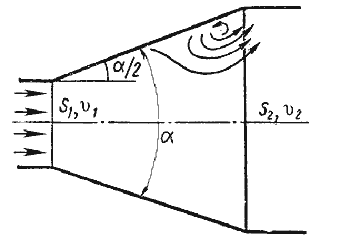
Расширяющаяся труба называется диффузором. Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Рисунок 25 – Постепенное расширение трубы

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

(25)

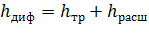
где h_тр и h_расш — потери напора на трение и расширение (вихреобразование).

(26)

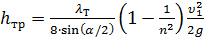
где n = S₂/S₁ = ( r₂/r₁ ) 2 — степень расширения диффузора. Потеря напора на расширение h_расш имеет ту же самую природу, что и при внезапном расширении русла

(27)

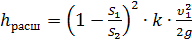
где k — коэффициент смягчения, при α= 5…20°, k = sinα.

Учитывая это полную потерю напора можно переписать в виде:

(28)

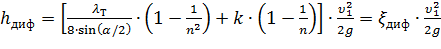
откуда коэффициент сопротивления диффузора можно выразить формулой

(29)

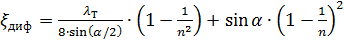
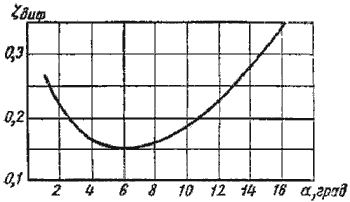
Рисунок 26 – Зависимость ζ_диф от угла

Функция ζ = f(α) имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:

(30)

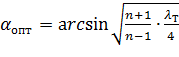
При подстановке в эту формулу λ_Т =0,015…0,025 и n = 2…4 получим α_опт = 6 (рисунок 26).

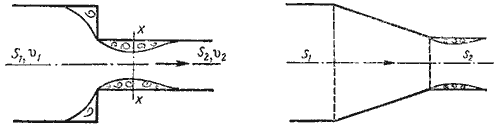
3. Внезапное сужение русла.

В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока.

Рисунок 27 – Внезапное сужение трубы

Рисунок 28 – Конфузор

Полная потеря напора определится по формуле:

(31)

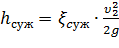
где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:

(32)

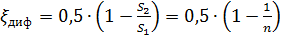
в которой n = S₁/S₂ — степень сужения.

При выходе трубы из резервуара больших размеров, когда можно считать, что S₂/S₁ = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζ_суж = 0,5.

4. Постепенное сужение русла.

Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рисунок 27). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение

(33)

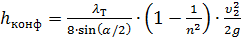
где коэффициент сопротивления конфузора определяется по формуле

(34)

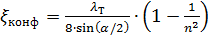
в которой n = S₁/S₂ — степень сужения.

Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рисунок 29).

Рисунок 29 – Сопло

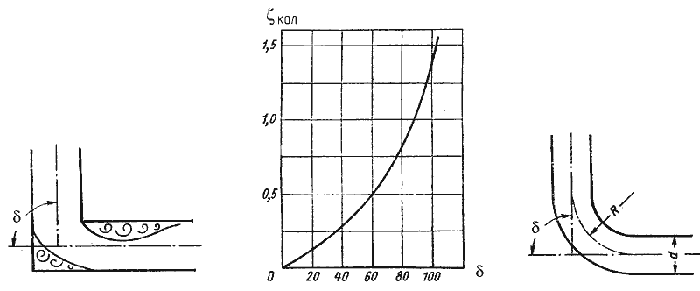
5. Внезапный поворот трубы (колено).

Данный вид местного сопротивления (рисунок 30) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

(35)

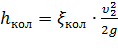
где ζ_кол — коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рисунок 31).

Рисунок 30 — Внезапный поворот трубы (колено).

Рисунок 31 — Зависимости ζкол от угла δ

Рисунок 32 – Отвод

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R/d рисунок 32). Коэффициент сопротивления отвода ζ_отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

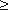
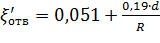
Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:

(36)

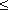
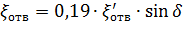
Для углов δ 70° коэффициент сопротивления

(37)

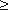
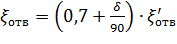
а при δ 100°

(38)

Потеря напора в колене определится как

(39)

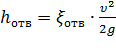
Иногда при расчете систем трубопроводов с большим числом местных сопротивлений потери напора в них вычисляют по их эквивалентным длинам. Длиной, эквивалентной данному местному сопротивлению, считается такая длина прямой трубы (того же диаметра, как и номинальный диаметр рассчитываемого трубопровода), на протяжении которой гидравлические потери равны потерям в данном сопротивлении. В результате такой замены все местные сопротивления в системе устраняются, длины труб соответственно увеличиваются и далее рассчитывается только прямолинейный трубопровод.

Пусть, например, надо заменить местное сопротивление С коэффициентом ζ трубой эквивалентной длины lэ диаметром d.
Значение эквивалентных длин для каждого значения ζ берется из таблиц соответствующих справочников. Таблицы КМС приведены в приложениях.

Для расчета характеристики участка составляем таблицу коэффициентов местного сопротивления циркуляционного кольца (таблица 22)

Таблица 22 – Ведомость коэффициентов местных сопротивлений циркуляционного кольца