Основы моделирования систем водоснабжения

Указанные книги не участвуют в акциях «Последняя бесплатно» и «Скидка на колличество купленных книг»

Количество книг в заказе: 0

Общая стоимость: 0 RUB

Общая стоимость с учетом скидки: 0 RUB

Пожалуйста, введите доступный Вам адрес электронной почты. По окончании процесса покупки Вам будет выслано письмо со ссылкой на книгу.

Список удаленных книг:

Список удаленных книг:

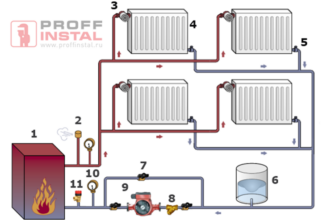
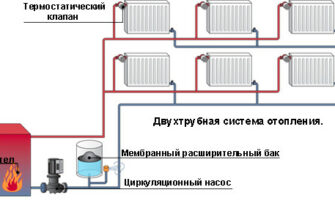
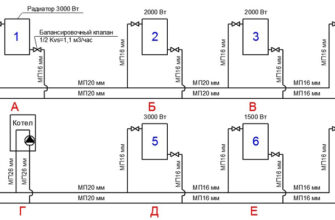
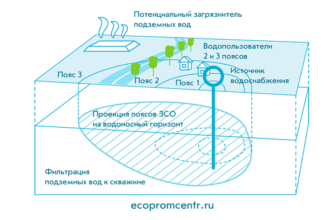
Рассмотрены основы моделирования процессов, связанных с системами водоснабжения и водоотведения. Обрисованы модели систем и рассмотрены методы их изучения. На изложенном материале студенты учатся методам математического моделирования, которые применяются в системах водоснабжения и водоотведения. Эти методы включают составление математического описания, выбор способа решения, программную реализацию модели и проверку адекватности модели реальному объекту. Для научных работников, архитекторов и инженеров в области градостроительного планирования реконструкции сложившейся жилой застройки 1950–1960-х гг., студентов, обучающихся по направлению 07.03.04 «Градостроительство», градостроителей, администрации поселений для управления реконструируемой жилой территорией, заказчиков-застройщиков, заинтересованных в инвестировании реконструкции жилой застройки.

Издатель:	Издательство МИСИ-МГСУ
Издатель:	Агентство электронных изданий «Интермедиатор»
Язык:	Русский
Публикация:	2017, Москва
Страниц:	126
ISBN:	978-5-7264-1641-.
УДК:	628.1
ББК:	38.761
К каталогам книги

57.00 p.

Страница недоступна для просмотра

h) или как следствие при соответствии между числом Маха 2 2 2 и числом Фруда для потока воды, т.е. M

/(gh) (где а — скорость звука). Методы газогидравлической аналогии в настоящее время интенсивно разрабатываются как для дозвукового, так и для сверхзвукового обтекания твердых тел. 1.3.4. Имитационное моделирование Существует достаточно много систем, для которых по различным причинам не разработаны аналитические модели или не разработаны методы их решения. В этом случае аналитическая модель заменяется моделью, с достаточной точностью описывающей реальную систему, с которой проводятся эксперименты. Экспериментирование с такой моделью называют имитацией, а саму модель — имитационной моделью. Имитационное моделирование это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно проигрывать во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов, однако по ним можно получить достаточно устойчивую статистическую картину системы. К настоящему времени сформировались три основные парадигмы имитационного моделирования. Причем каждая из них, первоначально возникшая для решения практических задач в достаточно ограниченных сферах, получив достаточное развитие, стала методологической основой имитационного моделирования. Парадигмы имитационного моделирования, абстрагированные от первоначально узко трактуемых понятий, приобрели универсальность, что значительно расширило область применения имитационного моделирования. При выбранном в качестве парадигмы моделирования дискретно-событийном моделировании в качестве парадигмы моделирования выступают абстрагирование от непрерывной природы событий и рассмотрение только основных событий моделируемой системы. Основоположником дискретно-событийного моделирования стал Дж. Гордон в 1960- х гг. Дискретно-событийное моделирование в настоящее время наиболее развито и имеет огромную сферу приложений: от логистики систем транспорта и массового обслуживания до промышленных систем. Этот вид моделирования наиболее подходит для производственных и производственно-технологических процессов. При системной динамике парадигмой моделирования является накопление массива данных об исследуемой системе в виде графических диаграмм причинных связей и глобальных влияний одних параметров 21 на другие во времени. В этом случае на основе полученного массива данных создается имитационная модель, работающая на компьютере. Этот подход основан Дж. Форрестером в 1950-х гг. По сути, такой вид моделирования более всех других парадигм помогает понять суть происходящего выявления причинно-следственных связей между объектами и явлениями. С помощью системной динамики можно создать модели развития города, его инженерных систем, экологических систем, динамики популяции, развития эпидемий и других динамических систем. новое, сформировавшееся в1990-х — 2000 — х гг. Агентное моделирование — направление имитационного моделирования. Название этого вида моделирования обусловлено понятием агент. Агент — некая сущность, обладающая активностью и автономным поведением. Агент может «принимать решения» в соответствии с некоторым набором правил, взаимодействовать с окружением (средой), а также самостоятельно изменяться в пределах системы. Парадигма агентного моделирования заключается в получении представлений об общих свойствах системы, исходя из положений об индивидуальном, частном поведении ее отдельных активных объектов и взаимодействии этих объектов в системе. Иными словами, подход к изучению динамики систем определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот, — глобальные правила и законы являются результатом индивидуальной активности элементов системы. Наибольшее распространение агентное моделирование получило в области исследования децентрализованных систем. Переходя от парадигм имитационного моделирования непосредственно к моделям, отметим, что общая классификация имитационных моделей в значительной мере схожа с классификацией систем, что естественно (рис. 1.1). ИМИТАЦИОННЫЕ МОДЕЛИ Статическая Дискретная Динамическая Непрерывная Детерминированная Стохастическая Рис. 1.1. Классификация имитационных моделей систем 22 это состояние системы в опреСтатическая имитационная модель — деленный момент времени или же системы, в которой время просто не играет никакой роли. Динамическая имитационная модель воспроизводит систему, меняющуюся во времени. Например, отражает состояние работы системы трубопроводов. имитационная модель не содержит вероятностных (случайных) компонентов, но ее аналитический аппарат решения чрезвычайно сложен. Стохастическая имитационная модель содержит случайные входные компоненты, в результате чего создается вероятностная действительность. Стохастические имитационные модели выдают результат, который является случайным сам по себе. Дискретная модель имеет те же признаки, что и дискретная система. Дискретная модель не всегда используется для моделирования дискретной системы, и наоборот. имеет сходные признаки с непреНепрерывная (событийная) модель рывной системой. Так, модель транспортного потока на автомагистрали будет дискретной, если необходимо учесть характеристики и движение отдельных машин. Однако если все машины можно рассматривать в совокупности, транспортный поток может быть описан с помощью дифференциальных уравнений в непрерывной модели. Дискретно-событийные имитационные модели отражают развитие системы во времени, когда переменные меняются мгновенно в конкретные моменты времени. В такие моменты времени происходят события, при этом событие определяется как мгновенное возникновение, которое может изменить состояние системы. С развитием достаточно мощных и компактных компьютеров имитационное моделирование позволяет не только решать научные проблемы, но и управлять сложными технологическими процессами в реальном времени. 1.4. Способы исследования систем Точные аналитические методы исследования систем и явлений охватывают ограниченный круг задач. В ряде случаев аналитическое решение сопряжено со значительными математическими трудностями, а часто строгая математическая постановка задачи оказывается невозможной из-за сложности исследуемого явления. Не всегда можно получить удовлетворительный результат и с помощью численных методов. В таких случаях на помощь приходят экспериментальные исследования на моделях реальных объектов. Для получения объективной информации о свойствах или состоянии системы необходимо проведение экспериментальных исследова23 ний. Какими бы совершенными ни казались теоретические представления об изучаемой системе, только результаты опытов могут подтвердить или опровергнуть их правильность. Поэтому эксперимент, безусловно, необходим, но с чем его проводить — с реальной системой или ее моделью? Если с моделью, то с какой? Рациональный подход к выбору типа эксперимента позволяет получить наиболее достоверные результаты при минимальных затратах времени и ресурсов. В принципиальном виде направления экспериментального изучения систем представлены на рис.1.2. ОПЫТ Эксперимент с реальной системой СИСТЕМА Эксперимент с моделью системы ОПЫТ Реальная модель Мнимая модель Физическая модель Математическая модель Имитационное моделирование Аналитическое решение Рис. 1.2. Структура направлений экспериментального изучения систем На начальном этапе планирования экспериментальных исследований стоит выбор, какой эксперимент проводить — с реальной системой или моделью системы? Сопоставим условия, при которых возможно проведение эксперимента, достоинства и недостатки обоих вариантов: я Проанализировав особенности экспериментов с физической и математической моделями и выбрав в качестве основы эксперимента математическое моделирование, определяют метод получения искомого результата — аналитическое решение или имитационное моделирование. Ниже сопоставлены условия, при которых возможно проведение эксперимента, достоинства и недостатки выбранных вариантов: Аналитическое решение Имитационное моделирование Условия проведения • математическая модель системы про- • математическая модель системы ста чрезвычайно сложна • исключается возможность аналитического решения • необходимость осуществить моделирование во времени Достоинства • возможно эффективное, в том числе • возможность моделирования во вребыстрое, решение «доступными» спо- мени собами • имитационное моделирование как «метод последней надежды» Недостатки • ограниченная область применения • потребность в мощных вычислительных ресурсах Важно отметить, что имитационное моделирование позволяет имитировать поведение системы во времени. Причем достоинством является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Вопросы для самопроверки 1. Каковы предпосылки для возникновения понятия моделирование и модель? 2. Какие виды моделей применяются в расчетах? 3. Что называется математической моделью? 4. Что называется физической моделью? 5. Какую роль играет эксперимент при инженерных решениях с использованием моделирования? 6. Какие глобальные модели Вы знаете? 7. Дайте определение моделированию. 8. Назовите ученых, внесших существенный вклад в развитие моделирования. Назовите основные предпосылки для выбора вида моделирования. 26 Глава 2. ТЕОРИЯ ПОДОБИЯ КАК ОСНОВА ФИЗИЧЕСКОГО МОДЕЛИРОВАНИЯ 2.1. Метод обобщенных переменных 2.1.1. Виды подобия Теория подобия — учение об условиях подобия физических явлений. Она опирается на учение о размерностях физических величин и служит основой физического моделирования. Главный принцип теории подобия — выделение из класса явлений (процессов), описываемых общим законом, группы подобных явлений. Подобными называют такие явления, для которых отношения сходственных и характеризующих их величин постоянны. Предметом теории подобия является установление подобия критериев различных физических явлений и изучение с их помощью свойств самих явлений. Физические явления, процессы или системы подобны, если в сходственные моменты времени в сходственных точках пространства значения переменных величин, характеризующих состояние одной системы, пропорциональны соответствующим значениям переменных величин другой системы. В теории подобия выделены четыре основных вида подобия (рис. 2.1). ВИДЫ ПОДОБИЯ Геометрическое Временное По физическим величинам По начальным и граничным условиям Рис. 2.1. Основные виды подобия Наиболее наглядный вид подобия — геометрическое, но в отличие от тригонометрического определения в теории подобия важно положение объектов в пространстве. 27 При размеры натуры и модели геометрическом подобии сходственные параллельны, а их отношения выражаются постоянной величиной: , где L , D , A — линейные размеры натуры; L , D , A — линейные разме0 0 0 1 1 1 ры модели; a — константа геометрического подобия, или масштабный l (переходный) множитель. Для динамических систем время имеет определяющее значение. Естественно, без этого параметра невозможно их моделирование. Поэтому в теории подобия существует понятие «временное (с ударением на о) подобие». временном подобии сходственные точки или части геометрически подобных систем (натуры и модели), двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени, отношение которых является постоянной величиной: , где и Т — время прохождения подобных путей сходственными точкаТ 1 ми объекта, натуры и модели, соответственно; и — время прохожде0 1 ния сходственными частицами подобных путей; a — константа временного подобия. При подобии физических величин (натуры и модели) отношение значений физических величин двух любых сходственных точек или частиц, подобно размещенных в пространстве и времени, есть величина постоянная: = а ; /ρ = а ; u /u = а , μ ρ 0 1 0 1 0 1 u где µ и µ , и , u и u — вязкость, плотность, гидравлическая круп0 1 0 1 0 1 ность натуры и модели, соответственно; a — константа подобия физиi величин. В общем случае ≠ ≠ а а а . μ ρ u Совокупность величин в области изучения называется полем величин. При соблюдении геометрического и временного подобия будет соблюдаться также подобие полей физических величин. Например, при кинематическом подобии существует подобие полей скоростей для двух рассматриваемых движений. При динамическом подобии реализуется подобие систем действующих сил или силовых полей различной физической природы (силы тяжести, силы давления, силы вязкости и т.п.). Механическое подобие, например, подобие двух потоков жидкости или газа, подобие двух упругих систем и т.п., предполагает наличие геометриче28 ского, кинематического и динамического подобий. Все перечисленные виды подобия — частные случаи физического подобия. При моделировании динамических систем необходимо учитывать не только уже рассмотренные виды подобия, но и изменения, происходящие в системе. Действительно, если сравнивать подобные модели, но находящиеся на разных стадиях изменения, то ряд констант не будут соответствовать их подобию. Для таких систем важен еще один вид подобия. При подобии начальных и граничных условий начальное состояние и состояние на границах систем (натуры и модели) подобны, а отношения основных параметров в начальный момент времени на границах систем постоянны. Только при подобии начальных и граничных условий соблюдается их геометрическое, временное и физическое подобие. 2.1.2. Инварианты и критерии подобия В подобных системах — натуре и ее моделях — в различных сходственных точках все константы подобия сохраняют постоянство: . Однако величины констант могут изменяться в зависимости от соотношения размеров натуры и модели. Из этого следует, что отношение однородных сходственных величин для натуры и другой модели, также подобной натуре, будет другим: . Это обстоятельство создает сложности для масштабирования и преодолевается введением понятия «инвариант подобия». Если все сходственные величины, определяющие состояние данной системы (натуры) и подобной ей системы (модели), измерять в относительных единицах, т.е. брать сходственное отношение величин для каждой системы, то оно также будет величиной постоянной и безразмерной: ; . Инвариантами подобия называются безразмерные числа, выражающие отношения размерных величин. Инварианты подобия, представляющие собой отношения однородных величин, называются симплексами или параметрическими критериями. Например, отношение геометрических величин в модели i = L /D , l 1 1 где i — геометрический симплекс. l 29 Инварианты подобия, выраженные отношением разнородных величин, называются критериями подобия. Для подобных гидравлических потоков безразмерные отношения одинаковы, что возможно только тогда, когда соответственные константы — безразмерные комплексы — также одинаковы: где Х — сила тяжести (по оси х); l — расстояние; u — скорость; p — 0 0 0 0 давление; — плотность; — кинематическая вязкость, индекс «0» означает характеристику одной системы. Приведенные безразмерные инварианты являются критериями динамического подобия гидравлических потоков: = Fr — критерием Фруда; (2.1) = Eu — критерием Эйлера; (2.2) = Re — критерем Рейнольдса; (2.3) = Ho = Sh — критерием гомохронности или критерием Струхаля. (2.4) Отметим физический смысл критериев динамического подобия движения вязкой несжимаемой жидкости. Безразмерные инварианты в структуре критериев характеризуют собой отношение сил различной физической природы к силам инерции. Так, коэффициент при первом слагаемом левой части уравнений (2.1) — (2.4) определяет отношение массовых сил к силам инерции, критерий Фруда является мерой отношения силы инерции к массовой силе. В поле силы тяжести — уравнение (2.2) — массовой силой является сама сила тяжести. В этом случае критерий Фруда характеризует отношение силы инерции к силе тяжести. Коэффициент при втором слагаемом уравнения (2.2) — критерий Эйлера — определяет отношение силы гид родинамического давления к силе инерции. Отношение силы инерции к силе трения (вязкости) характеризуется критерием Рейнольдса (2.3). Коэффициент при первом слагаемом правой части уравнения (2.4) раскрывает отношение между локальными и конвективными силами инерции — критерий Струхаля. Равенство определяющих безразмерных критериев натурного потока и потока на модели означает полное динамическое подобие рассматриваемых явлений. 1 При технических, в частности гидравлических, расчетах для упрощения понимания процесса используют следующие теоремы подобия, которые были выведены при экспериментальных исследованиях упомянутыми выше учеными: П е р в а я теорема подобия. Если явления подобны, то индикаторы подобия равны 1, у подобных явлений критерии равны между собой. В т о р а я теорема подобия. Зависимость между физическими величинами может быть представлена в виде зависимости между критериями подобия. Т р е т ь я теорема подобия. Подобны те явления, которые описываются одинаковыми уравнениями. 2.1.3. Автомодельность систем Независимость явления, процесса или, в общем случае, системы от какого-либо определенного критерия называется автомодельностью относительно этого критерия. Очевидно, эта независимость во всем диапазоне изменения критерия (в пределах рассматриваемой зоны автомодельности) предполагает, что изменение его функции не превышает наперед заданного малого значения. Например, с позиций теории подобия важными являются две области гидравлических сопротивлений по длине: зона ламинарного течения и зона квадратичного сопротивления. Первая зона, как это следует из экспериментальной зависимости =f(Rе), объединяет все опытные данные независимо от шероховатости трубопроводов. Во второй зоне коэффициент для фиксированной относительной шероховатости сохраняет постоянное значение. Таким образом, при изотермическом движении жидкости в напорном трубопроводе существуют две зоны автомодельности. Первая из них (область ламинарного течения) автомодельна по отношению к относительной шероховатости; вторая (квадратичная область) — автомодельна по числу Рейнольдса. Для ламинарного движения критерии Эйлера и Рейнольдса связаны соотношением Eu = idem / Re. В квадратичной области сопротивления силами вязкости можно пренебречь, поэтому для установившегося движения единственным критерием динамического подобия является критерий Эйлера. В этом случае и коэффициент также остается постоянным при всех значениях ≥ Rе Rе . Особенностью второй автомодельной области служит ракв коэффициентов сопротивления по длине для натурного потока и для потока на модели ( = ). Заметим, что высказанные соображен м ния оказываются справедливыми и для коэффициентов местных гидравлических сопротивлений. 32 2.1.4. Обобщенное критериальное уравнение В практике исследования или моделирования сложных многопараметрических систем часто возникают трудности в составлении математических описаний и в их преобразованиях в размерных величинах. Это неудобство преодолевается с помощью метода обобщенных переменных. зависимость между переменными, характеризующими какое- либо явление, может быть представлена в виде зависимости между критериями подобия: f (K , K , . К ) = 0, 1 2 i где K — критерии подобия (обобщенные переменные величины). i Эту зависимость называют обобщенным критериальным уравнением. Например, обобщенное критериальное уравнение гидродинамики имеет вид f (Ho, Eu, Fr, Re) = 0. Как видно из структуры уравнения, все его члены безразмерны и представляют собой комплексы величин — критерии, ответственные за определенные свойства системы или явления. Это позволяет существенно упростить модели систем и математические операции по моделированию и оценке результатов экспериментов. Важная особенность обобщенного критериального уравнения состоит также в том, что оно позволяет сократить число экспериментов при получении конкретных уравнений за счет варьирования критериев подобия, минуя определение всех величин. Наряду с очевидными преимуществами метода обобщенных переменных имеются ограничения, которые необходимо учитывать при его использовании. Наиболее существенные среди них следующие: • Используя методы теории подобия, нельзя получить информации больше, чем ее содержится в исходных уравнениях. • Если исходные уравнения неверно описывают физическую сущность процесса, то и полученные с использованием методов теории подобия зависимости будут неверны. • Полученные обобщенные уравнения обеспечивают достоверные результаты только в тех интервалах изменения переменных, которые были использованы при проведении эксперимента. • Моделирование на основе метода обобщенных переменных всегда связано с проведением эксперимента, иногда достаточно сложного, большого по объему и требующего значительных затрат времени. 33 2.2. Основы теории размерностей Предварительный качественный анализ и выбор системы безразмерных параметров может быть успешно произведен на основе теории размерностей и механического подобия. Использование этой теории дает возможность получить необходимый предварительный материал особенно для явлений, зависящих от большого числа параметров. При этом можно определить значимость каждого параметра и на этом основании исключить некоторые из них как несущественные из дальнейшего рассмотрения. Наиболее плодотворным является сочетание методов, основанных на теории размерностей и механическом подобии, с аналитическими методами. Напомним некоторые понятия, известные из курса физики. Принято различать размерные и безразмерные величины. Эти величины связаны между собой определенными соотношениями; при этом для некоторых из них могут быть произвольно назначены единицы измерения. Такие независимые физические величины называются основными, все остальные — производными. Выражение производной физической величины через основные физические величины называется размерностью. В механике в качестве основных физических величин принимают длину L, массу М и время Т; они независимы друг от друга. Для обозначения размерности обычно пользуются символической записью [а] (где а — произвольная физическая величина). Отметим, что любое физическое уравнение по размерности однородно, т.е. обе его части имеют всегда одинаковую размерность независимо от выбора системы физических величин. Это правило относится в пол- ной мере и к еще неизвестным уравнениям. Свойство однородности является основой теории размерностей. Пользуясь им, можно установить наличие, а иногда и вид зависимости между величинами, определяющими то или иное физическое явление. Формула размерности в разных системах физических величин для одной и той же величины может содержать различное число аргументов и может иметь различную форму. Поэтому о размерности можно говорить только применительно к определенной системе физических величин. Доказывается, что формулы размерности всех физических величин должны иметь вид степенных одночленов: x y z [D] = А B C , где D — производная величина; А, В, С — основные величины; х, у, z — показатели степени. Если можно на основании анализа того или иного явления выделить физические величины, полностью определяющие это явление, то установить характер зависимости между выделенными величинами удается 34 исходя из принципа однородности размерности с помощью так называемой -теоремы. Предположим, что какое-то явление полностью определяется конечным числом размерных физических величин. Функциональная зависимость между ними может быть представлена в виде , , . ) = 0, (2.5) f(А А А 1 2 n где A , А , . А — физические величины, определяющие рассматривае1 2 n мое явление; n — их число. Тогда в соответствии с -теоремой уравнение (2.5) будет выглядеть следующим образом: ( , , …, ) = 0, (2.6) 1 2 n–m где , , . — безразмерные независимые комбинации величин А; 1 2 n–m т — число основных физических величин. π Максимальное число независимых комбинаций при этом получается, если их структура представляется в виде (2.7) Или для любого числа , (2.8) где А — каждая последующая после А физическая величина от А до А ; i 3 4 n i = 4, 5, . Таким образом, при переходе от уравнения (2.5) к уравнению (2.6) сокращается число неизвестных от n до n–m. В механике, как уже говорилось, m = 3. Обращаясь к системе (2.7), заметим, что, как и для любого физического уравнения, размерность левой и правой частей ее уравнений должна π быть одинаковой. Поэтому, подставив число в виде произведения основных физических величин в нулевых степенях в правую часть уравнения (2.8), в соответствии с уравнениями (2.1) — (2.4) в виде степенного одночлена получим 35 Откуда или (2.9) где , , — числа, определяемые на основании однородности размер ности. Система (2.9) решается однозначно относительно неизвестных показателей степени х, у и z. Проводя последовательно аналогичные вычисления для каждой строки системы уравнений (2.7), определяем все безразмерные числа , , …, . 1 2 n–m Показатели степени x , y z по числовому своему значению у разных i i i π различны. Первые три физические величины А , А , А входят во все i 1 2 3 комплексы, а четвертая — всякий раз меняется при переходе от одного комплекса к другому. Следует иметь в виду, что если все величины, входящие в уравнение, являются кинематическими, то их размерность оределяется толь- ко двумя величинами (длина и время), поэтому в таком случае m = 2 и каждый комплекс составляется из (m + 1) величин, т.е. из трех соi для самопроверки 1. Назовите условия для создания достаточной близости подобия натуры и модели. 2. Какие критерии подобия Вы знаете? 3. Перечислите виды подобия. 4. Сформулируйте первую теорему подобия. 5. Сформулируйте вторую теорему подобия. 6. Сформулируйте третью теорему подобия. 7. Как определяются соотношения между масштабными коэффициентами? Какой критерий используется при динамическом подобии? 9. Приведите примеры подобия. 36 Глава 3. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМ 3.1. Основы процесса математического моделирования Самый сложный класс химико-технологических процессов — это процессы протекания химических реакций (реакционные процессы). Именно к ним наиболее важно применять методы математического моделирования. В первую очередь ниже будет рассмотрено моделирование реакционных процессов. В основе такого моделирования лежит описание химической реакции, соответствующее первому уровню иерархической структуры. Это описание складывается из описания стехиометрии, химического равновесия и кинетики. Стехиометрическое уравнение химической реакции (обычно его называют просто уравнением реакции) — это, как правило, самая первая информация, получаемая о ней химиком. Стехиометрическое уравнение представляет собой краткое выражение материального баланса реакции. Например, уравнение 2Н + О 2Н О (3.1) 2 2 2 означает, что всякий раз, когда в процессе реакции затрачиваются две молекулы Н , одновременно расходуется ровно одна молекула О и об2 две молекулы Н О. 2 Наряду с подобными записями «со стрелкой», часто пишут уравнения реакций со знаком равенства. Будем считать, что оба способа записи равноценны, и в разных случаях пользоваться тем из них, который оказывается удобнее. В большинстве случаев реагирующие вещества будем обозначать не конкретными формулами, а в общем виде: А, В, С, . J, . причем под символом J обычно будем понимать «какое-либо вещество»; то, что относится к J, можно отнести к любому из веществ. Иногда все вещества будем обозначать одной буквой А, различая индексами: A , А и т.д. 1 2 Стехиометрические коэффициенты в общем виде обозначим с индексом s вещества: s , s . A J В расчетах сложных реакций бывают случаи, когда уравнения целесообразно писать не только в привычном виде 2Н + О = 2Н О, 2 2 2 но и так: –2Н – О + 2Н О = 0 2 2 2 или, в общем виде, s A + s A + . + s A = 0. 1 1 2 2 m m 37 Причем в двух последних уравнениях разница между исходными веществами (реагентами) и продуктами реакции отражена в различных знаках стехиометрических коэффициентов. Обычно при таком способе записи считают, что для реагента или исходного вещества (расходуемого в реакции), s 0. Если реакция состоит из ряда стадий, то получается система из n уравнений: где i — номер вещества; m — общее количество веществ; n — число стадий. Разумеется, часть стехиометрических коэффициентов в любой строке может быть равна нулю. Стехиометрические расчеты особенно просты, когда количество вещества выражается в молях. Всюду, кроме особо оговоренных мест, будем выражать количество вещества g в молях, а концентрацию с — в молях на литр (или, что то же самое, в киломолях на кубометр). Рассмотрим реакцию, аналогичную выражению (3.1): 2А + В 2С. (3.2) Индексом 0 будем обозначать начальный момент (C — начальное J0 количество вещества J). Из уравнения реакции (3.2) для любого момента реакции вытекают следующие уравнения стехиометрического баланса: g + g = g + g ; (3.3) A С A0 С0 2g + g = 2g + g ; (3.4) B С B0 С0 2g – g = 2g – g . (3.5) B А B0 А0 Уравнение (3.3) выражает баланс реакции (3.1) по водороду: слева — удвоенное количество грамм-атомов Н в системе в текущий момент, справа — равное ему количество в момент начальный. Уравнение (3.4) выражает баланс по кислороду: первый член слева — количество грамм-атомов О в молекулах О (поскольку в каждой моле2 содержится два атома). Левая и правая части уравнения (3.5) равны избытку одного из реагентов сверх стехиометрии. Если в избытке будет О , то разность пол 9 3.2. Виды математических моделей Различаются следующие виды математических моделей. Модели, построенные на основе физико-химической сущности изучаемых процессов и явлений, называются детерминированными (аналитическими). Полученные в виде уравнений регрессии на основе обработки статистических и эксперементальных данных модели называются статистиче(эмпирическими). Наиболее универсальными являются скими физико-химические детерминированные модели. Физико-химическая детерминированная модель состоит из трех групп уравнений: • уравнения балансов массы и энергии — эта группа уравнений позволяет определить потоки массы и теплоты, изменение физико-химических свойств системы (вязкости, плотности и т.п.) в связи с изменением температуры и состава; • — эти уравнения дают описание химической уравнения кинетики кинетики, кинетики биологических превращений, тепло- и массопереноса и т.д. • уравнения состояния —уравнения этой группы описывают дисперсно-фазовые, молекулярно-дисперсные и другие равновесия. Физико-химические детерминированные модели обычно имеют более широкий интервал адекватности и поэтому получили наибольшее распространение при моделировании процессов очистки воды. Приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики, называется математической моделью. Математическая модель — мощный метод познания внешнего мира, а также прогнозирования и управления. Анализ математической модели позволяет проникнуть в сущность изучаемых явлений. Процесс математического моделирования, т.е. изучения явления с помощью математической модели, можно подразделить на четыре этапа. Первый этап — формулирование законов, связывающих основные объекты модели. Этот этап требует широкого знания фактов, относящихся к изучаемым явлениям, и глубокого проникновения в их взаимосвязи. Эта стадия завершается записью в математических терминах сформулированных качественных представлений о связях между объектами модели. Второй этап — исследование математических задач, к которым приводит математическое моделирование. Основным вопросом на данном этапе является решение прямой задачи, т.е. получение в результате анализа модели выходных данных (теоретических следствий) для дальнейшего их сопоставления с результатами наблюдений изучаемых явлений. На этом этапе важную роль приобретают математический аппарат, необходимый для анализа модели, и вычислительная техника — мощное сред40 ство для получения количества выходной информации как результата решения сложных математических задач. Часто математические задачи, возникающие на основе моделирования различных явлений, бывают одинаковыми (например, основная задача линейного программирования отражает ситуации различной природы). Это дает основание рассматривать такие типичные математические задачи, как самостоятельный объект, абстрагируясь от изучаемых явлений. Третий этап — выяснение того, удовлетворяет ли принятая гипотетическая модель критерию практики, т.е. выяснение вопроса о том, согласуются ли результаты наблюдений с теоретическими следствиями модели в пределах заданной точности наблюдений. Если модель была вполне определена, т.е. все параметры ее были заданы, то определение уклонений теоретических следствий от наблюдений дает решение прямой задачи с последующей оценкой уклонений. Если уклонения выходят за пределы точности наблюдений, то модель не может быть принята. Часто при построении модели некоторые ее характеристики остаются не определенными. Задачи, в которых определяются характеристики модели (параметрические, функциональные) таким образом, чтобы выходная информация была сопоставима в пределах точности наблюдений с результатами наблюдений изучаемых явлений, называются обратными задачами. Если математическая модель такова, что ни при каком выборе характеристик этим условиям нельзя удовлетворить, то модель непригодна для исследования рассматриваемых явлений. Применение критерия практики к оценке математической модели позволяет делать вывод о правильности положений, лежащих в основе подлежащей изучению (гипотетической) модели. Этот метод является единственным методом изучения недоступных нам непосредственно явлений макро- и микромира. Четвертый этап — последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели. В процессе развития науки и техники данные об изучаемых явлениях все более и более уточняются и наступает момент, когда выводы, получаемые на основании существующей математической модели, не соответствуют нашим знаниям о явлении. Таким образом, возникает необходимость построения новой, более совершенной математической модели. В понятие систематический, или системный, вкладывают смысл регулярного или строго последовательного. Под термином системный анализ можно понимать анализ в строгой последовательности. Речь идет об упорядоченной, связанной определенной последовательностью друг с другом совокупности предметов или вообще объектов, причем их упорядоченность подчинена некоторому заранее определенному назначению. Под системой понимается некоторое упорядоченное множество объектов или действий, объединенных единой целью или назначением. Каждому блоку или агрегату технологической схемы комплекса соответствует специфическая операция, т.е. если названа операция, то это ука 3 Как уже отмечалось выше, всякий блок системы определен технологической операцией. Разумеется, определение самой операции не входит в формальный язык математики. Это означает, что для построения математической модели блока совсем не достаточно выбрать формальный язык математики, его обязательно следует дополнить определением технологической операции в математической символике, например, с помощью дифференциальных уравнений. Переведенное таким способом на математический язык определение блока и будет его математической моделью. Математическую запись модели блока обычно называют формализацией соответствующего процесса, которая заключается в количественном изображении формальной стороны процесса в блоке через абстрагирование от его специального смысла. Как видно, формализация также обладает основным признаком моделирования, т.е. предполагает обязательное абстрагирование от второстепенного по отношению к основной цели. 3.3. Создание математической модели 3.3.1. Постановка задачи Для решения технологических и теоретических задач, стоящих перед исследователями, необходимо разработать модель, последовательность создания которой представлена на рис 3.1. 1. Постановка задачи 2. Анализ теоретических основ 3. Построение математической модели 4. Алгоритмизация математической модели 5. Параметрическая идентификация модели 6. Проверка адекватности математической модели 7. Моделирование системы 8. Анализ полученной информации Рис. 3.1. Последовательность создания математической модели 44 До сих пор говорилось о принципах моделирования, не затрагивая прагматической стороны вопроса. Для химика-технолога, а тем более для человека, занятого эксплуатацией комплекса водообеспечения, принципиальная сторона проблемы моделирования является далеко не основной. Главным же будет вопрос о практической применимости модели. Так зачем же строить математическую модель блока или системы? Без ответа на этот вопрос задача о моделировании системы водообеспечения превратится в самоцель, а это означает постановку под сомнение прагматической ценности всего системного анализа. Попробуем начать с более подробного анализа сущности формализации процесса. По определению, формализация дает количественные закономерности процесса в блоке. Это означает, что для заданных входных условий блока, используя формализацию процесса, всегда можно найти его результат на выходе. Например, пусть блок изменяет входную концентрацию компонента в К раз, т.е. формально процесс в блоке дается моделью = КС . Здесь, очевидно, дело связано с предсказанием С вых вх результата процесса в блоке по входным условиям и формальному представлению процесса. Другими словами, математическая модель позволяет прогнозировать работу блока. При прогнозировании с помощью модели, естественно, ничего нель- зя сказать о самом процессе, ведь формализация предполагает абстрагирование от внутреннего смысла процесса. То есть, жертвуя пониманием сущности процесса, приобретаем возможность предсказывать его результат. Такой подход во всем является типично прагматическим, устраивает как эксплуатационника, так и химика-технолога. Расширим теперь представление о прогнозе на случай зависимости от времени входных условий, которые принято называть внешним воздействием или просто воздействием на блок. Для заданной формализации процесса в блоке можно прогнозировать его результат на любой момент времени. Такой мгновенный результат воздействия называют откликом блока на воздействие. В принципе, процессом в блоке можно управлять, изменяя параметры формализации, определенным образом дозируя реагент, как-то воздействуя на гидродинамику потока. Такое управление отличается от воздействия своей целенаправленностью. Управление всегда можно согласовать с внешним воздействием так, чтобы отклик отвечал заданному условию, например, чтобы выходная концентрация компонента не превышала предельно допустимую при любом значении изменяющейся со временем входной концентрации. Управляемая технология оптимальна не только по параметрам отклика. Она позволяет экономить реагенты, в какой-то мере упрощает обслуживание комплекса, но самое главное — гарантирует высокую надежность эксплуатации. 45 3.3.2. Анализ теоретических основ Из изложенного становится очевидной следующая структура модели блока: Отклик – формализация воздействие. Такая структура допускает две возможности в формализации процесса. Во-первых, можно, абстрагируясь от квалификации типа процесса, формализовать его чисто эмпирической зависимостью отклика от воздействия. Для этого достаточно изменять по желанию экспериментатора воздействие и измерять отклик блока. Процесс в этом случае формализуется графической зависимостью, для которой всегда можно подобрать подходящую аналитическую форму, например, в виде многочлена. Подбор аналитической формы для экспериментального материала обычно выполняется специальными методами аппроксимации. Во-вторых, формализацию можно выполнить, опираясь на специфику процесса. Для физико-химических процессов такой спецификой может служить кинетика. Скорость изменения концентрации в замкнутом объеме согласно кинетическим представлениям пропорциональна концентрации в некоторой степени n. Порядок кинетики n существенно определен сложностью процесса, например, n = 1, если процесс идет в один этап: исходный продукт А переходит в конечный продукт В, который выводится из блока. Коэффициент пропорциональности (константа скорости) и порядок кинетики процесса можно найти в лабораторных исследованиях, так что при кинетической формализации процесса и вообще при формализации с известным аналитическим описанием процесса достаточно введения конструктивного определения блока, содержащего квалификацию гидродинамики или гидравлики процесса. Первый способ формализации, в отличие от второго, дается случайно подобранной закономерностью. Естественно, она описывает процесс с известным приближением. В этом смысле уместно ставить вопрос об адекватности (точности представления или изображения) процесса. Обычно дело обстоит так, что в экспериментально исследованной области адекватность модели вполне приемлема. Однако, если речь заходит о прогнозе за пределами этой области (экстраполяции), адекватность модели снижается, и тем сильнее, чем дальше выносится прогноз за пределы экспериментальной области. Второй способ свободен от этого недостатка во всей области прогнозирования, где можно гарантировать неизменность использованной для формализации закономерности, например кинетики процесса. В этом случае область адекватности модели устанавливается из общих соображений о специфике процесса как область, внутри которой точность формального описания процесса гарантирована его не46 изменным характером. Удобство второго способа состоит еще и в том, что общая закономерность, заложенная в основу формализации, содержит информацию о внутренней специфике процесса, чего полностью лишен первый способ. В прагматическом смысле это позволяет из самых общих соображений учитывать второстепенные факторы, которые могут влиять на процесс. 3.3.3. Построение математической модели Как уже отмечалось, построение модели начинается с введения корректного в конструктивном смысле определения блока. Пусть требуется построить модель реактора идеального смешения, процесс в котором формализуется кинетикой 1-го порядка. При этом под обобщенным понятием реактор будем иметь в виду любой блок системы водообеспечения, назначение которого целиком сводится к выведению определенного компонента из общего потока. Напомним, что реактором является емкость объемом V, в которой в результате перемешивания концентрация компонента не зависит от координат и процесс выведения компонента определен кинетикой первого порядка. Определение конструктивно уже потому, что дает распределение концентраций в объеме (неявное введение гидродинамики реактора) и формализует процесс кинетикой 1-го порядка. Построение модели начинается с введения уравнения материального баланса. Пусть m — поток массы компонента (масса за единицу времевх на входе реактора, m — выходной поток, m — поток, выводимый вых оc в результате деятельности реактора. Скорость изменения массы компонента в объеме реактора определится уравнением баланса массы , (3.8) смысл которого довольно проcт: скорость изменения массы компонента (точка над величиной — символ производной по времени) в объеме реактора равна разности потоков поступающей и выводимой масс. По определению, процесс в реакторе идет с кинетикой первого порядка. Поэтому , где константа скорости кинетики; k — m — масса компонента в объеме реактора. Поток массы связан с концентрацией компонента и расходом воды простым соотношением , откуда и . В силу независимости концентрации в объеме от координат масса компонента пропорциональна концентрации в объеме реактора, которая, в свою очередь, совпадает с С , т.е. С – С = m/V. Поэтому уравнение вых вых (3.8) переписывается в виде . (3.9) 47 В это уравнение удобно ввести два характерных времени: = Т V/Q 1 вых и Т = V/Q , первое из которых по смыслу соответствует времени полно2 осушения объема реактора при выходном расходе Q , второе — вревых заполнения его при входном расходе Q . Поделив (3.9) на объем вх реактора V, получим окончательную форму модели: (3.10) В модели (3.10) концентрация С совпадает с выходной по определению реактора и определяет отклик реактора на воздействие С , причем возвх в общем случае представляет собой достаточно произвольную функцию времени. Естественно, отклик реактора по (3.10) существенно определяется воздействием. Однако в отклике имеются и признаки, не зависящие от воздействия и присущие только реактору смешения как блоку со специальным назначением. Так, полагая в (3.10) = 0 (стационарный режим), легко найти простую связь выходной концентрации с входной: входная концентрация умножается на зависящую от расхода величину К = Т /Т (l + kT ), которая обязательно меньше едини1 2 1 цы; в результате этого получается выходная концентрация С = КС . вх вых Уменьшение входной концентрации как раз и является специфическим признаком отклика реактора. 3.3.4. Алгоритмизация математической модели Алгоритм — система операций, применяемых по строго определенным правилам для решения некоторой задачи. Обобщив сказанное, легко выработать простой алгоритм построения математической модели блока. Такой алгоритм относится исключительно к случаю формирования детерминированной модели и не может служить руководством к обработке экспериментальных данных. Один из его вариантов выглядит следующим образом: 1. По технологическим условиям формулируются гидродинамические условия прохождения потока через блок. 2. Определяется и формализуется процесс выведения компонента из состава воды в блоке. Оба этих шага алгоритма после их реализации дают определение блока. Блок может быть рассчитан на изменение временных характеристик потока, на его деление или суммирование (смешение) нескольких потоков. Поэтому вывод компонента из состава потока совсем необязателен, т.е. для определенных типов элементов технологической схемы формализация процесса выведения компонента сводится к констатации фак- та m = 0. ос 3. Составляется список потоков внесения и выноса компонента. 48 4. По результату п. 3 составляется уравнение материального баланса компонента в блоке. 5. По результату п. 2 и с помощью фундаментального соотношения m = CQ производится идентификация каждого члена уравнения материального баланса. После этого модель блока готова к использованию. Иногда возникает необходимость формализации п. 1. Подходящей формой связи входного и выходного расходов всегда может служить уравнение неразрывности потока воды. Приведенный алгоритм построения модели блока рассчитан только на один, хотя и отличающийся большой универсальностью, тип модели. Вместе с тем, для построения модели может быть использован любой подходящий язык, а это предполагает довольно большое количество способов формализации процессов в блоке. Как же выбрать подходящий способ моделирования для заданного перечня целей? Множеству загрязнений, входящих в состав воды, всегда можно поставить в соответствие некоторое множество способов их выведения, которое уже в какой-то мере описывает систему очистных сооружений и поэтому может служить ее моделью. Списку способов выведения компонентов можно поставить в соответствие технологическую схему комплекса и т.д. Как отмечалось выше, описание процесса выведения компонента любым способом представляет собой его моделирование. Из всего множества возможных моделей только некоторые допускают варьирование условий эксплуатации и перебор различных вариантов внутреннего устройства комплекса, и далеко не всякая модель позволяет количественно оценивать эффективность вариантов проекта или прогнозировать на количественном уровне влияние изменений условий эксплуатации. Например, надежность прогнозирования с помощью детерминированной математической модели предопределена самим принципом построения модели. Статистическая же модель позволяет достаточно надежно описывать процессы внутри области экспериментальных наблюдений, но быстро перестает быть адекватной за пределами этой области. Технологическая схема комплекса позволяет качественно прогнозировать результат перестановки блоков, что не обязательно соответствует методам удаления загрязняющих веществ. Когда на модели варьируются условия эксплуатации или изучаются варианты внутреннего устройства, имитируется сам комплекс в различных условиях его работы. Модель, допускающая такую имитацию, называется имитационной, или имитатором. Отбор варианта проекта должен быть связан с оценкой его эффективности. Это же относится и к выбору режима эксплуатации блока или системы. Влияние изменения внешних условий может быть оценено по зависимости от времени отклика блока или системы. Всем этим условиям 49 отвечает детерминированная математическая модель, что позволяет использовать ее в качестве имитатора блока или системы. Работа с имитатором дает возможность выбрать оптимальный режим эксплуатации или оптимальную конструкцию системы. Эксперименты с самим технологическим комплексом или его уменьшенной моделью не оправданы экономически и, кроме того, требуют чрезвычайно больших затрат времени. С этой точки зрения чрезвычайно выгодна и удобна имитационная модель системы. Схема процесса алгоритмизации модели представляет собой следующую последовательность: Полное математическое описание модели составление алгоритма изложение программы на языке ЭВМ. Наиболее сложным и ответственным этапом является составление полного математического описания модели (рис. 3.2). АНАЛИЗ ПАРАМЕТРОВ ЗАДАЧИ Размерность задачи Совокупность критериев для системы уравнений Наличие единственного решения Тип уравнений Простые Простые дифференциальные Дифференциальные в частных производных Рис. 3.2. Структура полного математического описания модели 3.3.5. Параметрическая идентификация модели Параметры математической модели — это коэффициенты, которые учитывают те или иные особенности натуры и характеризуют свойства данной натуры, отличающие ее от других натур подобного класса. Если часть параметров модели неизвестна, и оценить их значение можно только с помощью дополнительных экспериментов, то в этом случае необходимо провести параметрическую идентификацию модели. 50 Чем больше параметров входит в модель, тем подробнее и точнее можно описать и охарактеризовать данную натуру. Однако обработка многопараметрических математических моделей в значительной степени трудна и может сопровождаться экспериментальными ошибками. Процедура параметрической идентификации модели в достаточной степени формализована, о чем подробнее будет изложено в главе 4. 3.3.6. Проверка адекватности математической модели Ни одна модель в принципе не способна отразить оригинал полностью и всесторонне. Это положение вытекает из общефилософских соображений и одинаково верно как для материальных, так и для мысленных моделей. Более того, часто оказывается, что на практике целесообразнее пользоваться менее «совершенной» моделью, отражающей только отдельные черты оригинала и совсем не похожей на оригинал с других точек зрения. В ряде случаев целесообразно один оригинал моделировать при помощи разных моделей, не похожих одна на другую. Рассмотрим этот вопрос на простом примере. Предположим, необходимо смоделировать лабораторный стол для размещения опытных установок. Как должна выглядеть модель стола? Это зависит от того, какие вопросы желательно решать при помощи моделирования. это вопрос о механической прочности (скажем, на установках ожидаются удары большой силы), то основное требование — иметь возможность рассчитать силу удара, разрушающего оригинал. На этом этапе модель, возможно, воспроизведет только каркас, принимающий на себя нагрузки. Если решается вопрос о коррозионной стойкости материалов того же стола при воздействии веществ, которые могут выделиться при проведении опытов, то моделью будут служить просто кусочки материалов, погруженные в соответствующие среды. Такую модель и моделью-то обычно не называют, но, с точки зрения данного нами определения, это тоже модель. Если же необходимо заранее решить вопрос о наиболее удобном размещении стола в тесной лаборатории, то роль модели с успехом может выполнить бумажный прямоугольник, который можно двигать по плану лаборатории. Сходная особенность характерна и для мысленных моделей. Как и любая стадия познания, мысленная модель содержит в себе объективную истину, но не является абсолютной истиной. Вследствие сложности и многогранности любого явления природы часто оказывается целесообразным описывать и анализировать одно и то же явление, один и тот же объект в разных случаях при помощи разных моделей. Классическим 51 примером подобной ситуации является дуализм элементарных частиц. В зависимости от характера решаемой задачи поведение одних и тех же частиц описывается либо корпускулярной, либо волновой моделью. Важной особенностью мысленных моделей является то, что часто имеет смысл пользоваться упрощенной моделью даже в том случае, когда существует более совершенная. Это связано с тем обстоятельством, что чем проще модель, тем, как правило, проще сделать на ее основе количественные выводы. Зачастую бывает, что уточнение, получаемое при использовании более сложной модели, не оправдывает усложнения: иногда этим уточнением вообще можно пренебречь. В таких случаях стоит пользоваться упрощенными моделями. Примеров тому множество. В большинстве технологических расчетов свойств газов исходят из модели идеального газа, отлично зная, что реальные газы можно описать гораздо совершеннее. Но делать этого не стоит, поскольку точность, даваемая приближенной моделью, достаточна. И лишь при высоких давлениях, вблизи температуры конденсации или при высокоточных расчетах возникает необходимость в усложненных моделях. Сегодня есть модели молекулы гораздо более совершенные, чем модель Бутлерова. Несмотря на это, обычно молекулы изображаются «по Бутлерову». И лишь когда необходимо рассчитать энергетику молекулы или когда речь идет о веществах со сложными формами химической связи, таких как хелаты или ферроцен, насущно необходимыми становятся другие модели. Разумеется, если нужно достаточно точно описать сложный объект, следует применить сложную модель. В этих случаях получение полноценного математического описания — трудная задача, требующая большой работы. Но результат может оправдать все затраты. Ниже будет рассмотрен вопрос о сложности моделей, записываемых уравнениями или системами уравнений. Такие случаи встречаются наиболее часто (хотя, разумеется, модель может содержать и иные математические структуры — неравенства, алгоритмы, таблицы и пр.). Сложность уравнений может проявляться в разных формах. Во-первых, это число уравнений в системе. Во-вторых, это тип применяемых уравнений. Дифференциальные уравнения решать, как правило, сложнее, чем алгебраические; уравнения в частных производных — сложнее, чем· обыкновенные дифференциальные уравнения. Значительные сложности возникают при переходе от линейных уравнений к нелинейным. Системы линейных алгебраических или обыкновенных дифференциальных уравнений можно решить аналитически в общем виде (по крайней мере, когда этих уравнений не слишком много). Всякая нелинейность усложняет процедуру решения. Чаще всего простота или сложность математической модели связаны с тем, сколько в нее входит параметров — коэффициентов, учитывающих те или иные особенности объекта. Значения параметров характеризуют свойства данного конкретного объекта, отличающие его от других объек 3 3.3.7. Моделирование изучаемой системы Математическое моделирование, использующее аналогии, не свободно от трудностей, связанных с условиями подобия. Если оригинал сложен и условия подобия включают несколько критериев, то часто не удается создать модель, подобную оригиналу. Дальнейшее расширение возможностей моделирования связано со следующими соображениями. Уже говорилось, что в аналоговом моделировании модель и оригинал объединяет общность математической модели. Следующий шаг таков. Записав математическую модель оригинала, можно обработать ее на вычислительной машине. Если описание верно, то результаты, полученные на машине, можно количественно распространить на оригинал. Таким образом, рассмотренная процедура играет ту же роль, что и моделирование. Но на это можно возразить, напомнив, что моделирование определено как экспериментальное исследование материальной модели, здесь же — не эксперимент, а расчет. И где же материальная модель? Разумеется, решение задачи на ЭВМ — это расчет. Но в то же время не столь важно, как работает та или иная установка. Важнее, кто или что работает: приходится ли всю задачу решать человеку или значительная часть работы переложена на техническое устройство (модель или ЭВМ). В этом смысле применение ЭВМ имеет существенное сходство с моделированием: здесь на основе мысленной модели процесса (его математического описания) «организуется» некоторая установка — машина. Результаты работы этой установки распространяют на оригинал. Таким образом, вычислительную машину, рассчитывающую процесс на основе математического описания, можно считать материальной моделью исследуемого процесса. Поэтому применение вычислительной техники для анализа и расчета процессов на данном этапе обычно рассматривают как разновидность моделирования. Чаще всего этот способ моделирования называют математическим моделированием — в отличие от физического моделирования, при котором модель и оригинал физически идентичны, а основой построения модели служит теория подобия. Отметим, что при математическом моделировании соблюдаются оба основных требования к моделированию. Результат моделирования количественно распространяется на оригинал. Кроме того, моделирование дешевле, чем прямой эксперимент на оригинале. Правда, модель (ЭВМ) может быть и дороже оригинала, но это — модель универсальная, применяемая для моделирования очень многих оригиналов, и доля стоимости, приходящаяся на каждый из них, невелика. Необходимо иметь в виду, что нельзя противопоставлять физическое и математическое моделирование. Совсем бессмысленно считать, что одно из них лучше или хуже другого. Важно решить задачу, и на каждом этапе необходимо применять тот метод, который окажется более 54 эффективным. Выше рассказывалось о задачах, в которых нельзя (или, по крайней мере, весьма трудно) построить модель, подобную оригиналу. Разумеется, здесь необходимо моделирование математическое. С другой стороны, всей мощи современной «машинной математики» недостаточно для решения уравнения Навье — Стокса в сколько-нибудь сложных случаях — здесь без теории подобия не обойтись. Во многих случаях физический эксперимент просто оказывается дешевле сложного расчета, хотя возможно и то, и другое. И, наконец, необходимо иметь в виду, что, как правило, теория дает общий вид уравнений математического описания, а численные коэффициенты этих уравнений, значения которых отличают один частный случаи от другого (их называют параметрами математической модели), все равно должны быть найдены из опыта. Расшифровка на ЭВМ Термохимические опыты Кинетические опыты Мысленная модель химического процесса Ориентировочный выбор схемы и аппаратуры Тепловой стенд Математическое описание Диффузионный стенд процесса Гидравлический стенд Расчет оптимальных схем аппаратуры и режима на ЭВМ Опытная полупромышленная установка Уточненное математическое описание Расчет и оптимизация на ЭВМ Опытно-промышленная установка Рис. 3.3. Схема разработки технологического процесса 55 В целом при разработке нового химико-технологического процесса на различных этапах чередуется применение различных приемов моделирования, и каждый раз желательно оценить целесообразность применения того или иного из них. На рис 3.3 показана примерная (хотя не единственно возможная) схема разработки нового технологического процесса. Вначале проводят физико-химическое исследование, распадающееся на две основные части: 1) исследование равновесия и энергетики реакции и 2) исследование ее кинетики. В случае достаточно сложной реакции результаты этих опытов, как правило, обрабатывают при помощи ЭВМ. При этом уже с самого начала возникают обратные связи; ход обработки может показать, что опытных данных недостаточно или что какие-то из них нуждаются в уточнении. Таким образом, последующая стадия влияет на предыдущую. Подобные обратные связи возникают на всех этапах работы, хотя не все они показаны на схеме. Результатом обработки физико-химических опытов является мысленная модель химического процесса, включающая схему основных и побочных реакций, данные по равновесию, энергетике и кинетике и т.д. На основе этой мысленной модели осуществляют ориентировочный выбор технологической схемы и аппаратуры. Следующая стадия — моделирование основных сторон работы аппаратуры на стендах; в результате, привлекая также данные предыдущего этапа, получают математическую модель процесса в целом — с учетом влияния аппаратуры. Эту модель закладывают в машину и рассчитывают оптимальные размеры и режим опытной установки полупромышленного масштаба. Опыт работы этой установки позволяет внести уточнения в математическое описание и рассчитать уже большую, хотя, вероятно, еще опытную, установку. 3.3.8. Анализ полученной информации Анализ полученной информации сводится к изучению и проверке результатов, полученных при воспроизведении математической модели на ЭВМ. Любому не предполагаемому заранее решению необходимо дать рациональное объяснение, чтобы была гарантия от ошибок, которые могут возникнуть в результате вычислений. Кроме анализа непосредственно результатов, выдаваемых моделью системы, важно оценить работу самой модели. Для этого проводят анализ функционирования смоделированной натуры при изменении различных параметров. Анализ функционирования модели предполагает следующие цели: • изучение поведения модели при варьировании изменяющихся параметров; определение работоспособности данной модели при варьировании изменяющихся параметров и пределов работоспособности модели; 56 • ее работоспоусовершенствование модели для расширения диапазона собности и улучшения эксплуатационных показателей. На основании проведенного анализа принимают решение о выдаче рекомендации для практической реализации результатов моделирования или продолжении исследования. Анализ полученной информации по принятой модели может быть осуществлен методом математической статистики по критерию Фишера или критерию Стьюдента. Вопросы для самопроверки 1. Перечислите этапы математического моделирования. 2. Какая аналогия лежит в основе использования аналоговых вычислительных машин? 3. Найдите примеры аналогии, которые используют в областях химии и технологии, связанных с Вашей специальностью. 4. В чем состоит цель постановки задачи при моделировании? 5. Зачем создавать математическую модель блока или системы? 6. Опишите способы формализации процесса. 7. Дайте определение реактора. 8. Что называется алгоритмом математической модели? 9. Приведите структура полного математического описания модели. Глава 4. МЕТОДЫ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ СИСТЕМ 4.1. Основные понятия и определения статистического моделирования В последние годы интенсивно развивается математическая теория т.е. разрабатываются общие методы, позволяющие повыэксперимента, эффективность эксперимента практически во всех областях науки. Эта теория основывается на двух основных концепциях: • Концепция случайной ошибки. Нельзя грамотно поставить эксперимент и корректно обработать его результаты, не учитывая того, что (за ничтожным исключением) результаты любого эксперимента содержат случайные ошибки. • Концепция модели. Чтобы хорошо организовать эксперимент, в подавляющем числе случаев необходимо заранее знать (или хотя бы предполагать), в каком виде требуется получить описание объекта эксперимента, какая математическая модель будет построена по его результатам. 57 Для эффективного проведения эксперимента нужно заранее выбрать общий вид модели и сформулировать цель эксперимента. Рассмотрим основные понятия статистического моделирования. Случайной величиной в статистическом моделировании является та, точное значение которой в предстоящем измерении невозможно предсказать. В ряде задач величина случайна. В других задачах обычно трактуют величину как в основном неслучайную (детерминированную), но становящуюся случайной вследствие того, что при измерении на нее накладывается случайная ошибка. Однако провести четкую границу между теми и другими случайными величинами вряд ли возможно. В теории вероятностей различия между ними не делают. Главная характеристика случайной величины — вероятность. Вероятность Р есть число, заключенное между 0 и 1, характеризующее среднюю частоту появления в измерениях того или иного значения случайной величины. свойства функции f(u). Вероятность того, что U примет какое-либо значение в конечном интервале от до u , равна u 1 2 . В частности, можно рассмотреть случай u = –∞, т.е. вероятность того, 1 что U окажется не больше u : 2 . (4.1) Часто имеет смысл рассматривать верхний предел интеграла (4.1) как переменную. Тогда соответствующая вероятность становится функцией этого переменного верхнего предела: . (4.2) Функцию F(и) называют интегральной функцией распределения случайной величины U. Дифференциальная функция есть производная от интегральной: верхние пределы интегралов (4.1), (4.2) положить равными +∞, получим вероятность того, что величина U получит хоть какое-либо значение между –∞ и +∞. Это произойдет наверняка, поэтому . . y y y 0 0 0 х x a б в Рис. 4.1. Корреляционные графики для величин Х и Y: а — слабая отрицательная корреляция; б — сильная положительная корреляция; в — корреляция отсутствует В ряде задач анализ корреляции позволяет установить существенные связи, ценные для практики. Так, установив высокую положительную корреляцию между содержанием в рудах цинка и галлия, можно определить перспективный источник редкого элемента. Но во многих случаях корреляция связана с влиянием несущественных факторов, и ее наличие может даже помешать анализу сущности изучаемого явления. 4.2. Полный факторный эксперимент 4.2.1. Построение плана эксперимента В науке чаще всего измерения производятся таким образом, что из всей представляющей интерес совокупности объектов (генеральной совокупности) измеряется лишь некоторое сравнительно небольшое число (выборка). Связано это либо с тем, что генеральная совокупность слишком велика (обычно теоретически она бесконечна) и измерить все объекты невозможно (или, по крайней мере, слишком дорого), либо с тем, что процесс измерения разрушает объекты и проведение измерений на всей генеральной совокупности бессмысленно: она окажется полностью уничтоженной, так что выводы из эксперимента не к чему будет прилагать. Измерения на выборке проводятся для того, чтобы их результаты применить к генеральной совокупности. В этом смысле выборка есть модель генеральной совокупности, а измерения проводятся для того, чтобы в дальнейшем осуществить традукцию. В статистике это формулируется так: выборка должна быть представительной, т.е. давать возможность правильно судить о свойствах генеральной совокупности. Поэтому необходимо рассмотреть вопрос о том, насколько данные, получаемые по выборке, соответствуют генеральной совокупности. Рассчитываемые по результатам выборочных измерений числовые характеристики не совпадают в точности с соответствующими характери62 стиками генеральной совокупности. Кроме того, они — величины случайные, так как случаен сам отбор измеряемых объектов. Две выборки из одной и той же генеральной совокупности дадут несколько различающиеся значения числовых характеристик. Выборочные характеристики являются не точными значениями, а оценками характеристик генеральной совокупности; если источник случайности — ошибки измерений, то считают, что значения выборочных характеристик являются оценками истинных значений. Чтобы традукция оказалась правильной и по выборочным измерениям можно было верно судить о свойствах генеральной совокупности, рассчитываемые оценки должны обладать рядом свойств. Не давая строгих определений, укажем практический смысл этих свойств. Первое свойство — состоятельность. Состоятельной является оценка, которая при увеличении объема выборки сходится к генеральному значению: чем больше измерений, тем точнее характеризует наша оценка истинное значение, и при очень большом их числе оно может быть оценено со сколь угодно высокой точностью. Второе свойство — несмещенность. Несмещенная оценка при небольшом числе измерений может, разумеется, заметно отклоняться от оцениваемой величины, но в среднем она ей равна. В отличие от нее, смещенная оценка при малом числе измерений систематически отклоняется от оцениваемой величины (завышена или занижена), хотя при увеличении объема выборки может и стремиться к истинному значению, т.е. быть состоятельной. Несмещенность оценок очень важна в химии и химической технологии, где чаще всего эксперимент дорог и желательно работать с малыми выборками. Наконец, третье свойство оценок — эффективность: эффективная оценка точнее, чем любая другая оценка той же характеристики, полученная по той же выборке. На практике иногда приходится пользоваться оценками, не обладающими всеми этими свойствами, разумеется, если несостоятельность, смещенность и неэффективность достаточно малы, но этого желательно по возможности избегать. Оценкой математического ожидания М (Х) случайной величины Х является среднее арифметическое . (4.9) Нетрудно заметить, что формула (4.9) полностью аналогична выражению (4.3). В подавляющем большинстве случаев эта оценка — состоятельная, несмещенная и эффективная. Если теперь построить оценку дисперсии аналогично формуле (4.4) , 5 Аналогично строятся планы и при > 2. k Вопрос об оптимальности планов 2-го порядка сложен. В част н ости, в строгом смысле ортогональным такой план быть не может. Лишь спеα подбор величины и добавочное преобразование переменных позволяют получить ортогональность и избавиться от взаимной корреляции коэффициентов при квадратах факторов. Расчет параметров полиномов 2-й степени может проводиться либо по общим алгоритмам метода наименьших квадратов, либо по специально выведенным формулам. 4.2.2. Планирование и реализация полного факторного эксперимента Очень часто результаты эксперимента удается интерпретировать в терминах проверки гипотез. Обычная формулировка задачи здесь такова. Сопоставляются две выборки (или одна выборка сопоставляется с генеральной совокупностью). Формулируется нуль-гипотеза H : между обеими выборками нет 0 существенной разницы, обе они принадлежат одной генеральной совокупности, а имеющиеся различия обусловлены случайным характером выборок, например влиянием случайных ошибок. В этом случае любые оценки, рассчитанные по этим двум выборкам, будут оценками одних и тех же генеральных (истинных) значений; тогда в большинстве случаев имеет смысл объединить обе выборки в одну, увеличив тем самым число степеней свободы. При проверке гипотез возможны четыре ситуации. Первая — верна нуль-гипотеза, и ее принимаем; вторая — верна альтернативная гипотеза, и ее принимаем. В этих двух случаях решение правильное. В двух других случаях принято неверное решение (совершена ошибка). Если верна нуль-гипотеза, а ее отвергнем, принимаем альтернативную, — это ошибка 1-го рода. Если нуль-гипотеза неверна, а принята, — это ошибка 2-го рода. Разумеется, всегда есть желание принять верное решение. Однако в подавляющем большинстве случаев невозможно полностью исключить вероятность ошибки. Теоретически решение может быть совершенно безошибочным лишь тогда, когда окажется изученной вся генеральная совокупность, что может потребовать бесконечного числа измерений. Поэтому стоит задача — не исключить полностью ошибку, но сделать вероятность ошибки как можно более малой. Наиболее действенный, но и самый дорогой способ уменьшения ошибок — увеличение объема выборки, числа измерений. Чем больше измерений, тем надежнее выводы. Если количество измерений ограничено определенным числом, то имеется иной способ влияния на вероятность ошибок. Этот способ состоит в задании уровня строгости испытаний, под которым принимает76 ся решение о принятии либо , либо . Для этой ситуации характерH следующее. Чем строже испытание, тем больше вероятность ошибки 1-го рода и тем меньше — ошибки 2-го рода. При очень строгом испытании с большой вероятностью будет забракован даже годный объект, если по случайным причинам выборочные данные отклонятся от генерального значения. Напротив, при малой строгости испытания редко будут забракованы годные объекты и относительно часто будут признаны годными плохие. Практически чаще всего строгость испытания устанавливают, исходя из вероятности ошибки l-го рода. Эту вероятность называют уровнем α α значимости . Так, = 0,1 означает, что в данных условиях 10 % всех годных объектов будет забраковано (в среднем). На практике наиболее применим уровень значимости 0,05. Если особенно нежелательно допускать ошибки 2-го рода, можно применить более строгое испытание, на уровне значимости 0,1 или даже 0,2. Обычная процедура проверки гипотез заключается в следующем. По выборочным данным рассчитывается Полученное критерий проверки. значение критерия сравнивают с критическим значением, находимым из таблиц. Критическое значение каждого конкретного критерия определяется уровнем значимости и числом степеней свободы, по которому были рассчитаны величины, входящие в критерий. Таблицы критических значений имеются в многочисленных книгах по статистике и теории эксперимента. Рассмотрим четыре часто встречающихся критерия проверки гипотез. Эти критерии строго применимы к измерениям, ошибки которых имеют нормальный закон распределения; как уже сказано, обычно те же критерии применяют и в случаях, когда закон распределения неизвестен, но можно допустить, что он — нормальный. К ритерии исключения грубой ошибки Часто оказывается так, что в ряду измерений одной и той же величины один результат резко отличается от остальных: он заметно больше или заметно меньше. Можно предположить, что этот результат появился вследствие грубой ошибки, существенно превосходящей по абсолютной величине обычные случайные ошибки. Тогда данное измерение относится к иной генеральной совокупности, чем остальные. Но может быть и так, что грубой ошибки нет. Ведь нормально распределенная случайная величина может, хотя и редко, значительно отклониться от математического ожидания. Поэтому нуль-гипотеза заключается в том, что подозрительный результат относится к той же генеральной совокупности, что и остальные. Альтернативная гипотеза состоит в том, что этот результат порожден грубой ошибкой и должен быть исключен из дальнейшей обработки данных. 3 4.2.3. Анализ результатов полного факторного эксперимента Пусть в лабораторных условиях исследуются химические реакции в растворах. Изучается влияние трех факторов: u — концентрация моl %; u — концентрация инициатора полимеризации, %; u — тем2 К. Исходя из данных проводившихся ранее аналогичных опытов, намечены следующие условия: δ Факторы u i i u 24 4 l u 0,2 0,05 2 u 353 10 3 Отклик — выход фракции вещества. 3 Для опытов выбран план п.ф.э. 2 . Для оценки воспроизводимости в каждой точке плана (в каждой строке матрицы) проделаны по два опыта, результаты которых обозначены через у и у . Опыты рандомизованы, 1 2 но в приводимой ниже матрице даны по порядку. Пример 4.1. Определить однородность дисперсии по расширенной матрице плана эксперимента, содержащей столбцы всех взаимодействий. К матрице добавлены столбцы у , у , столбец -средних из у и у , а так1 2 1 2 2 же столбец s -дисперсий, полученных в каждой строке матрицы. Так как 2 каждая дисперсия s получена всего по двум измерениям (у и у ), ей соотj 2 ветствует число степеней свободы f = 1. Решение у у 2 x x x x x x x x x x x x x s 0 1 2 3 1 2 1 3 2 3 1 2 3 1 2 + – – – + + + – 63 61 62 2 + + – – – – + + 44 48 46 8 + – + – – + – + 54 55 54,5 0,5 + + + – + – – – 45 47 46 2 + – – + + – – + 54 54 54 0 + + – + – + – – 45 43 44 2 + – + + – – + – 51 53 52 2 + + + + + + + + 42 43 42,5 0,5 Обработку начинаем с проверки однородности дисперсий, поскольку лишь в случае однородных дисперсий вся дальнейшая обработка окажется корректной. Рассчитаем G (наибольшая дисперсия — во второй строке): 1. 84 Критическое значение = 0,680 (n = 8; = 1; = 0,05). Полученное G f кр значение меньше критического, следовательно, можно принять гипотезу однородности. Рассчитаем усредненную оценку дисперсии воспроизводимости (j = 8) по формуле (4.20): , . Теперь можно перейти к расчету коэффициентов регрессии. Расчет ведем по формуле (4.18), пользуясь средними : i Расчет дает: b = 50,125; b = –5,5; b = –1,375; b = + 1,00; b = + 0,625; 0 1 2 12 13 b = +0,5; b = –0,875 или 23 123 y = 50,125 – 5,5x – 1,375x – 2x + x x + 0,625x x + 0,5x x – 0,875x x x . 1 2 3 1 2 1 3 2 3 1 2 3 Это уравнение не позволяет проверить гипотезу об адекватности, по- тому что число коэффициентов в нем равно числу строк матрицы. В соответствии с формулой (4.19) число степеней свободы равно нулю. К тому же интерпретация уравнения — оценка характера влияния факторов — будет недостаточно надежной, если не исключить незначимые члены. Поэтому следующим этапом анализа будет проверка гипотезы о значимости коэффициентов регрессии. Рассчитаем дисперсию коэффициента по формуле (4.21): ; . По таблице критерия Стьюдента i = 2,31 (f = 8; = 0,05). Отсюда по формуле (4.22) b = 2,31 ∙ 0,364 = 0,841. i Таким образом, коэффициенты регрессии, меньшие по абсолютной величине, чем 0,841, можно считать незначимыми. Можно исключить 7 еще один остаток, равный –0,625, увеличив при этом число степеней свободы и для той, и для другой дисперсии на единицу, то получится (для случая уравнения без тройного взаимодействия): = 3,16; = 0,972; F = 3,16/0,972 = 3,25; F =3,63 (f = 4; f = 9; = 0,05). Такр образом, добавление центральной точки, увеличив число степеней свободы, подтвердило адекватность уравнения регрессии. Но можно получить и иные результаты: у у x x x у –у Р Р 1 2 3 1 2 0 0 0 57 55 56 50,125 +5,8755 В этом случае = 13,75; = 1,055; F = 13,0, и уравнение резко неадекватно. Ситуация, при которой уравнение, показавшее адекватность во всех точках плана 1-го порядка, оказывается неадекватным в центре плана, обычно бывает обусловлена влиянием членов, содержащих . Это значит, что план следует достроить до плана 2-го порядка. Вопросы и задания для самопроверки 1. Установлено, что два фактора, влияющие на процесс, коррелированны (коэффициент корреляции = 0,998). Какие можно дать рекомендации по планированию эксперимента на этом объекте? 2. Матрица планирования для двух факторов имеет вид x x x x 1 2 1 2 1 1 3 3 2 2 4 ? Какое число нужно подставить вместо вопроса, чтобы векторы-столбцы оказались ортогональными? 3. Дайте определение случайной величины. 4. Можно ли сказать, что среднеквадратичное отклонение случайной величины неизвестно? 5. Какой метод позволяет идентифицировать параметрическую модель? 88 Глава 5. МОДЕЛИРОВАНИЕ СТРУКТУРЫ ПОТОКОВ В СООРУЖЕНИЯХ 5.1. Основные понятия и определения показателей потока 5.1.1. Экспериментальное определение показателей потока в сооружениях Гидравлическое моделирование основано на общих законах подобия механических систем. Два потока жидкости подобны между собой, если они подобны геометрически, а также если для всех сходственных точек обоих потоков соблюдаются условия подобия их кинематических и динамических характеристик. В этом случае имеют место следующие равенства: = l; T = t; V = a = a ; P = p; υ l t н a м p = и = v υ н p м н м где L и l, Т и t, V и υ, а и а , Р и р, и и, наконец, v и v обозначают н м н м н м для натурного и модельного потоков длину, время, скорость, ускорение, силу (давление), плотность и коэффициент кинематической вязкости, а , , и т.д. — масштабные коэффициенты длины, времени, υ l t скорости и т.д. Обычно при моделировании потоков в сооружениях модельной жидкостью является вода той же плотности и вязкости, что и в натурном потоке, кроме того обычно опыты ведутся в условиях одного и того же значения g (g = g ), поэтому масштабные коэффициенты плотности, вязкости н м и ускорения свободного падения равны единице, т.е. = 1, = 1 и = 1. p v g В таких условиях точное подобие не соблюдается. Для достижения практически достаточной близости подобия натурного потока модельному необходимо соблюдать: • геометрическое подобие; • подобие начальных и граничных условий на модели; • равенство на модели и в натуре критериев динамического подобия, которые для проведения опытов должны быть выбраны в соответствии с основными силами, формирующими данный натурный поток. Соотношения между масштабными коэффициентами определяются по принятым критериям подобия. Можно составить следующие важнейшие соотношения: 89 которые обусловлены четырьмя наиболее часто используемыми критериями подобия: числом Фруда , числом Рейнольдса , числом Эйлера и числом Струхаля . Для медленных течений вязких жидкостей критерием подобия служит число Лагранжа, которое может быть представлено и как произведение чисел Эйлера и Рейнольдса: La = Eu · Re. При моделировании медленных течений вязких жидкостей необходимо обеспечить одновременно подобие сил вязкости и перепадов давле- ния. Основным критерием динамического подобия является критерий Ньютона , (5.1) т.е. для подобных потоков указанное число Ньютона должно быть оди н аковым. Из основного критерия Ньютона (5.1) можно получить частные критерии подобия для сил различной физической природы. Ниже приводятся наиболее часто встречающиеся в гидравлических задачах основные действующие силы и соответствующие им критерии подобия: силы тяжести — число Фруда ; силы вязкости — число Рейнольдса ; силы поверхностного натяжения — число Вебера ; силы давления — число Эйлера ; силы упругих деформаций (по Гуку) — число Коши ; силы инерции при неустановившемся движении — число Струхаля , υ — где скорость; l — длина; g — ускорение свободного падения; t — вреν — кинематическая вязкость; плотность; — давление; — P E сила деформации. Роль критериев подобия также могут играть любые другие параметры ( = ) и коэффициенты (С = С ), которые по условиям моделирован м н м ния в подобных системах сохраняют свое значение неизменным. Напри90 мер, при гидравлическом моделировании в условиях = и = , если g g н м н м пренебречь силами вязкости, масштабные коэффициенты = = 1 поg установить соотношения: при = 1 получаем и , υ g при = 1 получаем . Масштабные коэффициенты основных величин принято выражать в зависимости от линейного (геометрического) масштаба модели l (табл. 5.1). Табл. 5.1 удобно пользоваться для пересчета данных модельных испытаний на натуру. Таблица 5.1 Таблица для пересчета модельных испытаний на натуру Масштабные коэффициенты ускорения Условия скорости площади времени расхода объема длины силы моделирования По Фруду 1 По Рейнольдсу 1 Всякое физически обоснованное соотношение между размерными величинами можно сформулировать и представить как соотношение между безразмерными величинами — параметрами, которые в подобных системах могут играть роль критериев подобия. 5.1.2. Моделирование течений в напорных водоводах При моделировании движения жидкости критериальное уравнение в общем виде можно записать так: f (k/R, Re, Eu, St, Fr) = 0, (5.2) где k/R — относительная шероховатость стенок трубопровода, а остальные обозначения прежние. При напорном движении, когда объемные силы тяжести отсутствуют, критериальное уравнение (5.2) не содержит числа Фруда, а при установившемcя режиме из уравнения выпадает также критерий St и оно принимает вид f (k/R, Re, Eu) = 0. (5.3) 1 91 В состав критерия Эйлера входит перепад давлений, величина которого неизвестна, следовательно, определяющим критерием является число Re и из зависимости (5.3) можно получить условия моделирования в форме Eu = f (k/R; Re), (5.4) или, имея в виду, что , в форме λ = f (k/R; Re) при Re = idem. Условия моделирования существенно облегчаются при наличии двух автомодельных зон: • зоны ламинарного режима весьма медленных течений вязких жидкостей, когда можно пренебречь инерционными силами. Подобие устанавливается по критерию Лагранжа La = Eu · Re = idem, что приводит к условию Eu = idem / Re; • зоны квадратичного сопротивления при Re > Re , когда можно м пр пренебречь силами вязкости и принять k/R = const. Условия подобия определяют при . В этом случае задача моделирования сводится к подбору шероховатоλ λ сти русла на модели, чтобы обеспечить условие = .Сравнительно ман м лое измерение коэффициента сопротивления в переходной зоне шероховатых труб рассчитывают по формуле где R и k — гидравлический радиус и высота выступов шероховатости м м на модели. α Масштабные коэффициенты для всех физических величин можно 1 установить на основе формул (5.4) и (5.5). α λ Принимая линейный масштаб по условиям шероховатости = f(Rе), l α α с учетом Rе = Rе , можно определить масштабные коэффициенты , υ м пр q и α — для скорости, расхода и давления. ∆p 92 Для гладких водоводов подобие устанавливают при условии что приводит к соотношениям масштабных коэффициентов 5.1.3. Моделирование равномерных течений в открытых каналах Общий вид критериального уравнения для экспериментального определения любой физической величины имеет вид a = f (Fr, Re). i λ λ Для условий автомодельности при = моделировать можно при н м условии Соотношения между масштабными коэффициентами при Fr = idеm (см. табл. 5.1) приводят к условию . При моделировании по Фруду (Fr = idem) строгое подобие нарушаетλ если сопротивление потока на модели больше, чем в натуре (λ > ). м н λ За пределами области автомодельности = f(Rе) определяющим критерием становится также число Рейнольдса (Re = idem). 5.1.4. Специальные вопросы моделирования М оделирование размывов при аварии водовода При моделировании размывов необходимо совместно рассматривать λ) критерии динамического подобия потока в водоводе (Fr, Re, Ка, с параметрами и критериями подобия размываемости и деформации грунта υ ρ’; (H /H; /υ* ; Re ), критериями взвешивания и переноса частиц пор пр пр * υ υ — 2 током (υ/ω ; /ρ’gh), где Ка — число Кармана; скорость. 0 В табл. 5.2 представлены примеры моделирования водных потоков в различных условиях. 93 Таблица 5.2 Примеры моделирования водных потоков при их взаимодействии с частицами твердыми Условия моделирования Область автомодельности Масштабные зависимости Общий вид Моделируемое функциональной явление Условия зависимости при полном с искажением подобия Величина и критериального Вид числа Rе геометрическом геометрических пр уравнения Re пр подобии масштабов Размываемость 60—75 α ≠ α ≠ α русла l h d при грядовой 10—12 структуре дна α = α = α l h d γ ω f (ρ’u , d, , µ, ) = 0 ∗ 1 0 α = α = α = 1 ρ’ i λ Ф (Fr ; Re ; )=0 Re > Re 1 d м пр α ≠ 1 при α ≠ 1 или ρ’ Re > Re Размываемость 300 ∗м ∗пр ρ’ α ≠ α ≠ 1 1 каналов λ i α = α = α = d Re м 1 5.2. Модели структуры потоков 5.2.1. Общие представления о моделях структуры потоков Поведение потоков в реальных установках настолько сложное, что в настоящее время дать его строгое математическое описание в большинстве случаев не представляется возможным. В то же время известно, что структура потоков оказывает существенное влияние на эффективность процессов, поэтому ее необходимо учитывать при моделировании процессов. При этом математические модели структуры потоков являются основой, на которой строится математическое описание химико- технологического процесса. Наиболее существенными источниками неравномерности распределения элементов потока по времени пребывания в промышленных аппаратах являются: • неравномерность профиля скоростей системы; • турбулизация потоков; • наличие застойных областей в потоке; • каналообразование, байпасные и перекрестные токи в системе; • температурные градиенты движущихся сред; • тепло- и массообмен между фазами и т.п. Истинное время пребывания в сооружении частиц потока может оказаться недостаточным для осуществления процесса диффузии, а от этого зависит эффективность всего диффузионного процесса в целом. Поэтому важным является учет реальной структyры потоков фаз в аппарате, а следовательно, и учет времени их пребывания в аппарате с помощью модельных представлений о внутренней структуре потоков. Для процессов массопередачи описание структуры потоков имеет еще и тот смысл, что позволяет установить перемещение и распределение ве- ществ в этих потоках. Поэтому все гидродинамические модели потоков записываются в виде уравнений, определяющих изменение концентрации вещества в потоке. 5.2.2. Модель идеального вытеснения Идеальные потоки, как и любая идеализация, — это абстракция, которую нельзя точно осуществить на практике. Однако ясность физической картины и простота математического описания идеальных потоков делают эти модели чрезвычайно удобными для анализа протекания химических процессов. В аппарате идеального вытеснения поток движется совершенно равномерно. В любом поперечном сечении все частицы имеют одинаковую скорость (рис. 5.1). Фронт потока движется, как твердый поршень. Поэтому такой поток иногда называют поршневым (от англ. piston-flow). 102 Фронт потока Вход потока Выход потока Поршневой поток Рис. 5.1. Схема потока идеального вытеснения При анализе сложных процессов (например реакций, проходящих с выделением и отводом тепла) определение идеального вытеснения приходится несколько конкретизировать. Добавляется еще одно свойство. Не только скорость, но и концентрации и температуры в таком потоке выровнены по поперечному сечению. Для изотермических процессов эта выровненность получается автоматически, если выровнены скорости. Среднее время пребывания текущей жидкости в аппарате определяется простым соотношением , (5.10) υ — где V — объем аппарата (точнее, его рабочей зоны); объемный расa жидкости. Для описания, анализа и расчета процессов существенны два следствия из определения идеального вытеснения: • Время пребывания всех частиц в потоке идеального вытеснения одинаково. Это практически единственный мыслимый поток, для которого формула (5.10) дает не только среднее время пребывания, но и конкретное время пребывания любой движущейся через аппарат частицы жидкости. Малый объем Вход потока Выход потока Рис. 5.2. Схема малого объема смеси, движущейся в потоке идеального вытеснения 1