Расчет диаметра трубы наружного водоснабжения
В этой статье я расскажу вам о том, как профессионально посчитать диаметр трубы. Будут указаны полезные формулы. Вы узнаете какой диаметр трубы вам нужен для водопроводных труб. Также очень важно не путать, расчет подбора диаметра трубы для водоснабжения, от расчета для отопления. Так как для отопления бывает достаточно низкого потока движения воды. Формула расчета диаметра труб кардинально отличаются, так как для водоснабжения необходимы большие скорости потока воды.
О том, как рассчитать диаметр трубы для отопления описано тут: Расчет диаметра трубы для отопления
Что касается таблиц для расчета диаметра трубы, то об этом будет рассказано в других статьях. Скажу лишь то, что данная статья вам поможет найти диаметр труб без таблиц, по специальным формулам. А таблицы придуманы просто, упростить процесс вычисления. К тому же в этой статье Вы поймете, из чего складывается весь результат необходимого диаметра.
Чтобы получить расчет диаметра трубы для водоснабжения, необходимо иметь готовые цифры:
| — Расход потребления воды. — И потери напора от точки А до точки Б, пути трубопровода до точки потребления. |
Что касается расхода потребления воды , то тут примерно есть приблизительно готовый цифровой стандарт. Возьмем к примеру смеситель в ванной. Я опытным путем проверил, что для комфортного потока воды на выходе примерно равно: 0,25 литров в секунду. Эту величину и возьмем для стандарта по подбору диаметра для водного потока.
Есть еще одна не маловажная цифра. В квартирах это обычно стандарт. У нас в стояках для водоснабжения примерно стоит давление напора: Около 1,0 до 6,0 Атмосфер. В среднем это 1,5-3,0 атмосфер. Это зависит от этажности многоквартирного дома. В многоэтажных домах свыше 20 этажей, стояки могут быть разделены по этажности, чтобы не перегружать нижние этажи.
А теперь давайте приступим к алгоритму расчета необходимого диаметра трубы для водоснабжения. В этом алгоритме есть неприятная особенность, это то, что нужно делать расчет циклично подставляя в формулу диаметр и проверяя результат. Так как в формуле потерь напора существует квадратичная особенность и в зависимости от диаметра трубы резко изменяется результат потерь напора. Я думаю, больше трех циклов нам не придется делать. Также еще зависит от материала трубопровода. И так приступим!
| |
Вот некоторые формулы, которые помогут найти скорость потока:
| S-Площадь сечения м 2 π-3,14-константа — отношение длины окружности к ее диаметру. r-Радиус окружности, равный половине диаметра Q-расход воды м 3 /с D-Внутренний диаметр трубы |
0,25л/с=0,00025м 3 /с
V=(4*Q)/(π*D 2 )=(4*0,00025)/π*0,012 2 =2,212 м/с
Далее находим число Рейнольдса по формуле:
ν=1,16*10 -6 =0,00000116. Взято из таблици. Для воды при температуре 16°С.
Δэ=0,005мм=0,000005м. Взято из таблици, для металлопластиковой трубы.
Далее сверяемся по таблице где находим формулу по нахождению коэффициента гидравлического трения.
У меня подпадает в первую область и я принимаю для расчета формулу Блазиуса.
λ=0,3164/Re 0,25 =0,3164/22882 0,25 =0,0257
Далее используем формулу для нахождения потерь напора:
| h-потеря напора сдесь она измеряется в метрах. λ-коеффициент гидравлического трения. L-длина трубопровода измеряется в метрах. D-внутренний диаметр трубы, то есть диаметр потока жидкости. Должен быть вставлен в формулу в метрах. V-скорость потока жидкости. Измеряется [Метр/секунда]. g-ускорение свободного падения равен 9,81 м/с 2 |
h=λ*(L*V 2 )/(D*2*g)=0,0257*(10*2,212 2 )/(0,012*2*9,81)=5,341 м.
И так: На входе у нас 2 атмосферы, что равно 20 метрам напора.
Если полученый результат 5,341 метров меньше входного напора, то результат нас удовлетворяет и диаметр трубы с внутренни диаметром 12мм подходит!
Если нет то необходимо увеличивать диаметр трубы.
Но имейти ввиду, если в расчет брать трубу, которая из подвала идет по стоякам к вам на пятый этаж, то результат возможно будет не удовлетворительным. А если у вас саседи будут отбирать поток воды, то и соответственно входной напор может уменьшится. Так что имейти ввиду про запас в два три раза уже хорошо. В нашем случае запас в четыре раза больше.
Давайте попробуем так ради эксперимента. У нас в трубе 10 метров в пути, имеются четыре угольника (колена). Это гидравлические сопротивления и они называются местными гидравлическими сопротивлениями. Для колена в 90 градусов имеется формула расчета:
| h-потеря напора сдесь она измеряется в метрах. ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. V-скорость потока жидкости. Измеряется [Метр/секунда]. g-ускорение свободного падения равен 9,81 м/с2 |
h=ζ*(V 2 )/2*9,81=0,249 м.
Так как у нас 4 угольника, то полученый результат умножаем на 4 и получаем 0,996 м. Почти еще один метр.
Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м. То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м 3 /ч. Температура воды 16°С. Найти максимально возможный расход в конце трубы.
| D=100 мм = 0,1м L=376м Геометрическая высота=17м Отводов 21 шт Напор насоса= 0,5 МПа (50 метров водного столба) Максимальный расход=90м 3 /ч Температура воды 16°С. Труба стальная железная |
Найти максимальный расход = ?
Для решения необходимо знать график насосов: Зависимость расхода от напора.
В нашем случае будет такой график:
Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.
По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м 3 /час. (90-Qmax=14 м 3 /ч).
Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).
Поэтому решаем задачу ступенчато.
Поскольку мы имеем интервал расходов от 0 до 76 м 3 /час, то мне хочется проверить потерю напора при расходе равным: 45 м 3 /ч.
Находим скорость движения воды
Q=45 м 3 /ч = 0,0125 м 3 /сек.
V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с
Находим число рейнольдса
ν=1,16•10 -6 =0,00000116. Взято из таблици. Для воды при температуре 16°С.
Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.
Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.
У меня попадает на вторую область при условии
10•D/Δэ 0.25 =0,11•( 0,0001/0,1 + 68/137069) 0,25 =0,0216
Далее завершаем формулой:
h=λ•(L•V 2 )/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.
Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:
Теперь делаем оригинальный расчет при расходе равный 64м 3 /час
Q=64 м 3 /ч = 0,018 м 3 /сек.
V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с
λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/197414) 0,25 =0,021
h=λ•(L•V 2 )/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.
Отмечаем на графике:
Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).
Ответ: Максимальный расход равен 54 м 3 /ч. Но это мы решили без сопротивления на поворотах.
Для проверки проверим:
Q=54 м 3 /ч = 0,015 м 3 /сек.
V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
Итог: Мы попали на Нпот=14,89=15м.
А теперь посчитаем сопротивление на поворотах:
Формула по нахождению напора на местном гидравлическом сопротивление:
| h-потеря напора здесь она измеряется в метрах. ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. V-скорость потока жидкости. Измеряется [Метр/секунда]. g-ускорение свободного падения равен 9,81 м/с2 |
ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.
Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.
Скорость 1,91 м/с
h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м.
Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.
Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.
Давайте теперь решим целиком задачку с отводами.
При расходе 45 м 3 /час получили потерю напора по длине: 10,46 м. Смотри выше.
При этой скорости (2,29 м/с) находим сопротивление на поворотах:
h=ζ•(V 2 )/2•9,81=(1•2,29 2 )/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.
Складываем потери напора: 10,46+5,67=16,13м.
Отмечаем на графике:
Решаем тоже самое только для расхода в 55 м 3 /ч
Q=55 м 3 /ч = 0,015 м 3 /сек.
V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.
Складываем потери: 14,89+3,78=18,67 м
Рисуем на графике:
Ответ: Максимальный расход=52 м 3 /час. Без отводов Qmax=54 м 3 /час.
Чтобы в ручную не считать всю математику я приготовил специальную программу:
Калькулятор расчета оптимального диаметра трубопроводов
Оптимальный диаметр трубопровода – это наиболее подходящий минимальный диаметр для перемещения необходимого объема жидкости с точки А в точку Б. Правильный расчет и выбор оптимального диаметра, также оптимизирует ваши денежные затраты.
Формула для расчета оптимального диаметра трубы имеет следующий вид:
dо = √((4·Q) / (π·Vо))
do – оптимальный диаметр трубопровода
Vo – оптимальная скорость потока
Q – заданный расход перемещаемой жидкости
Как видите она не такая уж сложная, но все же предлагаем вам воспользоваться специально разработанным по данной формуле калькулятором.
Калькулятор оптимального размера диаметра трубопроводов по расходу воды, жидкости и др
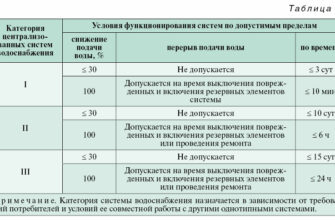
| Среда в трубопроводе | Диапазон оптимальных скоростей в трубопроводе, м/с |
| Движение самотеком: | |
| Вязкие жидкости | 0,1 – 0,5 |
| Маловязкие жидкости | 0,5 – 1 |
| Перекачивание насосом: | |
| Всасывающая сторона | 0,8 – 2 |
| Нагнетательная сторона | 1,5 – 3 |
| Естественная тяга | 2 – 4 |
| Малое давление | 4 – 15 |
| Большое давление | 15 – 25 |
| Перегретый пар | 30 – 50 |
| Пар под давлением: Более 105 Па | 15 – 25 |
| Пар под давлением: (1 – 0,5) · 105 Па | 20 – 40 |
| Пар под давлением: (0,5 – 0,2) · 105 Па | 40 – 60 |
| Пар под давлением: (0,2 – 0,05) · 105 Па | 60 – 75 |
Калькулятор расчета производительности трубы
Расчет производительности трубы производят по формуле Q = (π·d²)/4 · v
Данные производительности трубы необходимы для расчета оптимального диаметра трубопровода