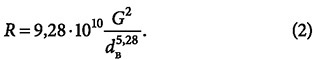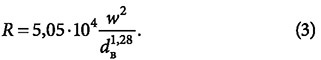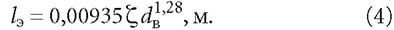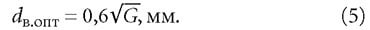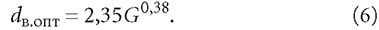Скорость воды в системе отопления нормы

Скорость воды в системе отопления нормы

Скорость воды в системе отопления нормы

Диаметр трубопроводов, скорость течения и расход теплоносителя.

Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И какие связи между ними. В других материалах будет подробный расчет диаметра для отопления.

Для того чтобы вычислить диаметр необходимо знать:

1. Расход теплоносителя (воды) в трубе. 2. Сопротивление движению теплоносителя (воды) в трубе определенной длины.

Вот необходимые формулы, которые нужно знать:

S-Площадь сечения м 2 внутреннего просвета трубы π-3,14-константа – отношение длины окружности к ее диаметру. r-Радиус окружности, равный половине диаметра, м Q-расход воды м 3 /с D-Внутренний диаметр трубы, м V-скорость течения теплоносителя, м/с

Сопротивление движению теплоносителя.

Любой движущийся внутри трубы теплоноситель, стремиться к тому, чтобы прекратить свое движение. Та сила, которая приложена к тому, чтобы остановить движение теплоносителя – является силой сопротивления.

Это сопротивление, называют – потерей напора. То есть движущийся теплоноситель по трубе определенной длины теряет напор.

Напор измеряется в метрах или в давлениях (Па). Для удобства в расчетах необходимо использовать метры.

Для того, чтобы глубже понять смысл данного материла, рекомендую проследить за решением задачи.

В трубе с внутренним диаметром 12 мм течет вода, со скоростью 1м/с. Найти расход.

Решение: Необходимо воспользоваться вышеуказанными формулами:

1. Находим сечение 2. Находим расход

D=12мм=0,012 м п=3,14

S=3.14•0,012 2 /4=0,000113 м 2

Q=0,000113•1=0,000113 м 3 /с = 0,4 м 3 /ч.

Имеется насос, создающий постоянный расход 40 литров в минуту. К насосу подключена труба протяженностью 1 метр. Найти внутренний диаметр трубы при скорости движения воды 6 м/с.

Q=40л/мин=0,000666666 м 3 /с

Из выше указанных формул получил такую формулу.

Каждый насос имеет вот такую расходно-сопротивляемую характеристику:

Это означает, что наш расход в конце трубы будет зависеть от потери напора, которое создается самой трубой.

Чем длиннее труба, тем больше потеря напора. Чем меньше диаметр, тем больше потеря напора. Чем выше скорость теплоносителя в трубе, тем больше потеря напора. Углы, повороты, тройники, заужения и расширение трубы, тоже увеличивают потерю напора.

Более детально потеря напора по длине трубопровода рассматривается в этой статье:

А теперь рассмотрим задачу из реального примера.

Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м. То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м 3 /ч. Температура воды 16°С. Найти максимально возможный расход в конце трубы.

D=100 мм = 0,1м L=376м Геометрическая высота=17м Отводов 21 шт Напор насоса= 0,5 МПа (50 метров водного столба) Максимальный расход=90м 3 /ч Температура воды 16°С. Труба стальная железная

Найти максимальный расход = ?

Решение на видео:

Для решения необходимо знать график насосов: Зависимость расхода от напора.

В нашем случае будет такой график:

Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.

По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м 3 /час. (90-Qmax=14 м 3 /ч).

Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).

Поэтому решаем задачу ступенчато.

Поскольку мы имеем интервал расходов от 0 до 76 м 3 /час, то мне хочется проверить потерю напора при расходе равным: 45 м 3 /ч.

Находим скорость движения воды

Q=45 м 3 /ч = 0,0125 м 3 /сек.

V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с

Находим число рейнольдса

ν=1,16•10 -6 =0,00000116. Взято из таблици. Для воды при температуре 16°С.

Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.

Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.

У меня попадает на вторую область при условии

10•D/Δэ 0.25 =0,11•( 0,0001/0,1 + 68/137069) 0,25 =0,0216

Далее завершаем формулой:

h=λ•(L•V 2 )/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.

Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:

Теперь делаем оригинальный расчет при расходе равный 64м 3 /час

Q=64 м 3 /ч = 0,018 м 3 /сек.

V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с

λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/197414) 0,25 =0,021

h=λ•(L•V 2 )/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.

Отмечаем на графике:

Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).

Ответ: Максимальный расход равен 54 м 3 /ч. Но это мы решили без сопротивления на поворотах.

Для проверки проверим:

Q=54 м 3 /ч = 0,015 м 3 /сек.

V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с

λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213

h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.

Итог: Мы попали на Н_пот=14,89=15м.

А теперь посчитаем сопротивление на поворотах:

Формула по нахождению напора на местном гидравлическом сопротивление:

h-потеря напора здесь она измеряется в метрах. ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. V-скорость потока жидкости. Измеряется [Метр/секунда]. g-ускорение свободного падения равен 9,81 м/с2

ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.

Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.

Скорость 1,91 м/с

h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м.

Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.

Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.

Давайте теперь решим целиком задачку с отводами.

При расходе 45 м 3 /час получили потерю напора по длине: 10,46 м. Смотри выше.

При этой скорости (2,29 м/с) находим сопротивление на поворотах:

h=ζ•(V 2 )/2•9,81=(1•2,29 2 )/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.

Складываем потери напора: 10,46+5,67=16,13м.

Отмечаем на графике:

Решаем тоже самое только для расхода в 55 м 3 /ч

Q=55 м 3 /ч = 0,015 м 3 /сек.

V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с

λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213

h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.

h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.

Складываем потери: 14,89+3,78=18,67 м

Рисуем на графике:

Ответ: Максимальный расход=52 м 3 /час. Без отводов Qmax=54 м 3 /час.

В итоге, на размер диаметра влияют:

1. Сопротивление, создаваемое трубой с поворотами 2. Необходимый расход 3. Влияние насоса его расходно-напорной характеристикой

Если расход в конце трубы меньше, то необходимо: Либо увеличить диаметр, либо увеличить мощность насоса. Увеличивать мощность насоса не экономично.

Данная статья является частью системы: Конструктор водяного отопления

Скорость движения воды в трубах системы отопления.

Thượng Tá Quân Đội Nhân Dân Việt Nam

Ох и дурют там вашего брата!
Ты чего хочешь-то? “Военную тайну” (как на самом деле надо делать) узнать, или курсовик сдать? Если только курсовик – то по методичке, которую преподаватель и написал и ничего иного не знает и знать не хочет. И если сделаешь как надо, еще и не примет.

1. Есть минимальная скорость движения воды. Это 0.2-0.3 м/с, из условия удаления воздуха.

2. Есть максимальная скорость, которая ограничивается, чтобы трубы не шумели. Теоретически это надо расчетом проверять и некоторые программы это делают. Практически же знающие люди пользуются указаниями старинного СНиП еще 1962 года, где была таблица предельных скоростей. Оттуда и по всем справочникам разошлось. Это 1,5 м/с при диаметре 40 и более, 1 м/с для диаметра 32, 0,8 м/с для диаметра 25. Для более мелких диаметров были другие ограничения но потом на них наплевали.

Допустимая скорость и теперь есть в пукте 6.4.6 (аж до 3 м/с) и в приложении Ж СНиП 41-01-2003, только “доценты с кандидатами” постарались, чтобы бедные студенты не смогли разобраться. Там и к уровню шума привязано, и к кмс и к прочей хрени.

Но допустимая – это совсем не оптимальная. Про оптимальную в СНиП вообще не упоминается.

3. Но все-таки есть и оптимальная скорость. Не какая-то 0,8-1,5, а самая настоящая. Вернее, не сама скорость, а оптимальный диаметр трубы (скорость-то не сама важна), причем с учетом всех факторов, включая металлоемкость, трудоемкость монтажа, комплектации да и гидравлической устойчивости.

Вот секретные формулы:

0.037*G^0.49 – для сборных магистралей
0.036*G^0.53 – для стояков отопления
0.034*G^0.49 – для ммагистралей ветки, пока нагрузка не уменьшится до 1/3
0.022*G^0.49 – для концевых участков ветки с нагрузкой в 1/3 от всей ветки

Здесь везде G – расход в т/ч, а получается внутренний диаметр в метрах, который надо округлить до ближайшего большего стандартного.

Ну, а правильные пацаны вообще никакими скоростями не задаются, а просто делают в жилых домах все стояки постоянного диаметра и все магистрали постоянного диаметра. Но тебе еще рано знать, какие именно диаметры.

Скорость теплоносителя в системе отопления

Гидравлический расчёт системы отопления с учетом трубопроводов.

Гидравлический расчёт системы отопления с учетом трубопроводов.

При проведении дальнейших расчетов мы будем использовать все основные гидравлические параметры, в том числе расход теплоносителя, гидравлическое сопротивление арматуры и трубопроводов, скорость теплоносителя и т.д. Между данными параметрами есть полная взаимосвязь, на что и нужно опираться при расчетах.

К примеру, если повысить скорость теплоносителя, одновременно будет повышаться гидравлическое сопротивление у трубопровода. Если повысить расход теплоносителя, с учетом трубопровода заданного диаметра, одновременно возрастет скорость теплоносителя, а также гидравлическое сопротивление. И чем больше будет диаметр трубопровода, тем меньше будет скорость теплоносителя и гидравлическое сопротивление. На основе анализа данных взаимосвязей, можно превратить гидравлический расчет системы отопления (программа расчета есть в сети) в анализ параметров эффективности и надежности работы всей системы, что, в свою очередь, поможет снизить расходы на использующиеся материалы.

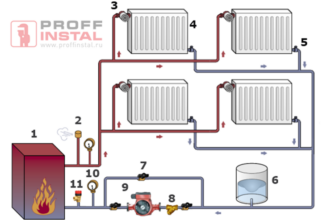
Отопительная система включает в себя четыре базовых компонента: теплогенератор, отопительные приборы, трубопровод, запорная и регулирующая арматура. Данные элементы имеют индивидуальные параметры гидравлического сопротивления, которые нужно учесть при проведении расчета. Напомним, что гидравлические характеристики не отличаются постоянством. Ведущие производители материалов и отопительного оборудования в обязательном порядке указывают информацию по удельным потерям давления (гидравлические характеристики) на производимое оборудование или материалы.

Например, расчет для полипропиленовых трубопроводов компании FIRAT существенно облегчается за счет приведенной номограммы, в которой указываются удельные потери давления или напора в трубопроводе для 1 метра погонного трубы. Анализ номограммы позволяет четко проследить обозначенные выше взаимосвязи между отдельными характеристиками. В этом и состоит основная суть гидравлических расчетов.

Гидравлический расчет систем водяного отопления: расход теплоносителя

Думаем, вы уже провели аналогию между термином «расход теплоносителя» и термином «количество теплоносителя». Так вот, расход теплоносителя будет напрямую зависеть от того, какая тепловая нагрузка приходится на теплоноситель в процессе перемещения им тепла к отопительному прибору от теплогенератора.

Гидравлический расчет подразумевает определение уровня расхода теплоносителя, касательно заданного участка. Расчетный участок представляет собой участок со стабильным расходом теплоносителя и с постоянным диаметром.

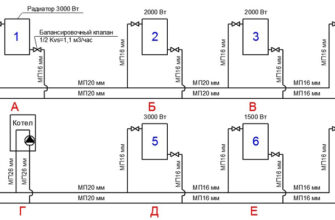
Гидравлический расчет систем отопления: пример

Если ветка включает в себя десять киловаттных радиаторов, а расход теплоносителя рассчитывался на перенос энергии тепла на уровне 10 киловатт, то расчетный участок будет представлять собой отрезом от теплогенератора до радиатора, который в ветке является первым. Но только при условии, что данный участок характеризуется постоянным диаметром. Второй участок располагается между первым радиатором и вторым радиатором. При этом, если в первом случае высчитывался расход переноса 10-киловаттной тепловой энергии, то на втором участке расчетное количество энергии будет составлять уже 9 киловатт, с постепенным уменьшением по мере проведения расчетов. Гидравлическое сопротивление должно рассчитываться одновременно для подающего и обратного трубопровода.

Гидравлический расчет однотрубной системы отопления подразумевает вычисление расхода теплоносителя

для расчетного участка по следующей формуле:

Qуч –тепловая нагрузка расчетного участка в ваттах. К примеру, для нашего примера нагрузка тепла на первый участок будет составлять 10000 ватт или 10 киловатт.

с (удельная теплоемкость для воды) – постоянная, равная 4,2 кДж/(кг•°С)

tг –температура горячего теплоносителя в отопительной системе.

tо –температура холодного теплоносителя в отопительной системе.

Гидравлический расчет системы отопления: скорость потока теплоносителя

Минимальная скорость теплоносителя должна принимать пороговое значение 0,2 — 0,25 м/с. Если скорость будет меньше, из теплоносителя будет выделяться избыточный воздух. Это приведет к появлению в системе воздушных пробок, что, в свою очередь, может служить причиной частичного или полного отказа отопительной системы. Что касается верхнего порога, то скорость теплоносителя должна достигать 0,6 — 1,5 м/с. Если скорость не будет подниматься выше данного показателя, то в трубопроводе не будут образовываться гидравлические шумы. Практика показывает, что оптимальный скоростной диапазон для отопительных систем составляет 0,3 — 0,7 м/с.

Если есть необходимость рассчитать диапазон скорости теплоносителя более точно, то придется брать в расчет параметры материала трубопроводов в отопительной системе. Точнее, вам понадобится коэффициент шероховатости для внутренней трубопроводной поверхности. К примеру, если речь идет о трубопроводах из стали, то оптимальной считается скорость теплоносителя на уровне 0,25 — 0,5 м/с. Если трубопровод полимерных или медный, то скорость можно увеличить до 0,25 – 0,7 м/с. Если хотите перестраховаться, внимательно почитайте, какая скорость рекомендуется производителями оборудования для систем отопления. Более точный диапазон рекомендованной скорости теплоносителя зависит от материала трубопроводов применяемых в системе отопления а точнее от коэффициента шероховатости внутренней поверхности трубопроводов. Например для стальных трубопроводов лучше придерживаться скорости теплоносителя от 0,25 до 0,5 м/с для медных и полимерных (полипропиленовые, полиэтиленовые, металлопластиковые трубопроводы) от 0,25 до 0,7 м/с либо воспользоваться рекомендациями производителя при их наличии.

Расчет гидравлического сопротивления системы отопления: потеря давления

Потеря давления на определенном участке системы, которую также называют термином «гидравлическое сопротивление», представляет собой сумму всех потерь на гидравлическое трение и в локальных сопротивлениях. Данный показатель, измеряемый в Па, высчитывается по формуле:

ΔPуч=R* l + ( (ρ * ν2) / 2) * Σζ

ν — скорость используемого теплоносителя, измеряемая в м/с.

ρ — плотность теплоносителя, измеряемая в кг/м3.

R –потери давления в трубопроводе, измеряемые в Па/м.

l – расчетная длина трубопровода на участке, измеряемая в м.

Σζ — сумма коэффициентов локальных сопротивлений на участке оборудования и запорно-регулирующей арматуры.

Что касается общего гидравлического сопротивления, то оно представляет собой сумму всех гидравлических сопротивлений расчетных участков.

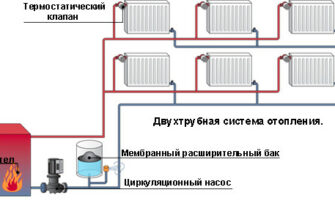
Гидравлический расчет двухтрубной системы отопления: выбор основной ветви системы

Если система характеризуется попутным движением теплоносителя, то для двухтрубной системы выбирается кольцо самого загруженного стояка через нижний прибор отопления. Для однотрубной системы – кольцо через самый загруженный стояк.

Если система характеризуется тупиковым движением теплоносителя, то для двухтрубной системы выбирается кольцо нижнего прибора отопления для самого загруженного из наиболее удаленных стояков. Соответственно, для однотрубной отопительной системы выбирается кольцо через наиболее загруженный из удаленных стояков.

Если речь идет о горизонтальной отопительной системе, то выбирается кольцо через наиболее загруженную ветвь, относящуюся к нижнему этажу. Говоря о загрузке, мы имеем в виду показатель «тепловая нагрузка», который был описан выше.

[content-egg module=GdeSlon template=compare]

Скорость движения воды в трубах системы отопления.

На лекциях нам говорили, что оптимальная скорость движения воды в трубопроводе 0,8-1,5 м/с. На некоторых сайтах встречаю подобное (конкретно про максимальную в полтора метра в секунду).

НО в методичке сказано принимать потери на метр погонный и скорости – по приложению в методичке. Там скорости ну совсем другие, максимальная, что есть в табличке – как раз 0,8 м/с.

И в учебнике встретил пример расчета, где скорости не превышают 0,3-0,4 м/с.

Дак в чем же суть? Как вообще принимать (и как в реальности, на практике)?

Скрин таблички из методички прилагаю.

За ответы всем заранее спасибо!

Ты чего хочешь-то? “Военную тайну” (как на самом деле надо делать) узнать, или курсовик сдать? Если только курсовик – то по методичке, которую преподаватель и написал и ничего иного не знает и знать не хочет. И если сделаешь как надо, еще и не примет.

0.036*G^0.53 – для стояков отопления

0.034*G^0.49 – для ммагистралей ветки, пока нагрузка не уменьшится до 1/3

0.022*G^0.49 – для концевых участков ветки с нагрузкой в 1/3 от всей ветки

В курсовике то я посчитал как по методичке. Но хотел узнать, как по делу обстановка.

Тоесть получается в учебнике (Староверов, М. Стройиздат) тоже не верно (скорости от 0,08 до 0,3-0,4). Но возможно там только пример расчета.

Offtop: Тоесть вы тоже подтверждайте, что по сути старые (относительно) СНиПы вполне ничем не уступают новым, а где то даже лучше. (нам об этом многие преподаватели говорят. По ПСП вообще декан говорит, что их новый СНиП во многом противоречит и законам и самому себе).

Но в принципе все пояснили.

а расчет на уменьшение диаметров по ходу потока вроде экономит материалы. но увеличивает трудозатраты на монтаж. если труд дешевый-возможно имеет смысл. если труд дорогой – никакого смысла нет. И если на большои длине (теплотрасса) изменение диаметра выгодно -в пределах дома возня с этими диаметрами не имеет смысла.

и еще есть понятие гидравлическои устойчивости системы отопления – и здесь выигрывают схемы ShaggyDoc

Каждый стояк (верхняя разводка) отключаем вентилем от магистрали. Дак вот встречал, что сразу после вентиля ставят краны двойной регулировки. Целесообразно?

И чем отключать сами радиаторы от подводок: вентилями, или ставить кран двойной регулировки, или и то и то? (тоесть если бы этот кран мог полностью перекрывать трупровод – то вентиль тогда вообще не нужен?)

И с какой целью изолируют участки трубопровода? (обозначение – спиралью)

Система отопления двухтрубная.

Мне конкретно по подающему трубопроводу узнать, вопрос выше.

У нас есть коэффициент местного сопротивления на вход потока с поворотом. Конкретно применяем на вход через жалюзийную решетку в вертикальный канал. И коэффициент этот равен 2,5 – что есть не мало.

Тоесть как бы так придумать, чтобы избавиться от этого. Один из выходов – если решетка будет “в потолке”, и тогда входа с поворотом не будет (хотя небольшой все же будет, так как воздух будет стягиваться по потолку, двигаясь горизонтально, и двигаться к этой решетке, поворачивать на вертикальное направление, но по логике это должно быть меньше, чем 2,5).

В многоквартирном дме решетку в потолке не сделаешь, соседи. а в одноквартирном – потолок не красивый с решеткой будет, да и мусор может попасть. тоесть проблему так не решить.

часто сверлю, потом затыкаю

Возьмите тепловую мощность и начальную с конечной температуры. По этим данным Вы совершенно достоверно посчитаете

скорость. Она, скорее всего, будет максимум 0.2 мС. БОльшие скорости – нужен насос.

Нормативы должен знать каждый: параметры теплоносителя системы отопления многоквартирного дома

Жители многоквартирных домов в холодное время года чаще доверяют поддержание температуры в комнатах уже установленным батареям центрального отопления.

В этом преимущество городских многоэтажек перед частным сектором — с середины октября и до конца апреля коммунальные службы заботятся о постоянном обогреве жилых помещений. Но не всегда их работа безупречна.

Многие сталкивались с недостаточно горячими трубами в зимние морозы, и с настоящей тепловой атакой весной. На самом деле, оптимальная температура квартиры в разное время года определена централизованно, и должна соответствовать принятому ГОСТу.

Нормативы отопления ПП РФ № 354 от 06.05.2011 и ГОСТ

6 мая 2011 года было издано Правительственное Постановление, которое действует по сей день. Согласно ему, отопительный сезон зависит не столько от времени года, сколько от температуры воздуха на улице.

Центральное отопление начинает работать при условии, что внешний термометр показывает отметку ниже 8 °C, и похолодание длится не менее пяти суток.

На шестой день трубы уже начинают обогрев помещений. Если в течение указанного времени наступило потепление, отопительный сезон откладывается. Во всех частях страны, батареи радуют своим теплом с середины осени и поддерживают комфортную температуру до конца апреля.

Если морозы наступили, а трубы остаются холодными, это может быть результатом неполадок в системе. В случае глобальной поломки или незавершённых ремонтных работ придётся воспользоваться дополнительным обогревателем, пока неисправность не будет устранена.

Если проблема заключается в заполнивших батареи воздушных пробках, то обращаются в эксплуатирующую компанию. В течение суток после подачи заявки приедет закреплённый за домом сантехник и «продует» проблемный участок.

Стандарт и нормы допустимых значений температуры воздуха прописаны в документе «ГОСТ Р 51617-200. Жилищно-коммунальные услуги. Общие технические сведения». Диапазон прогрева воздуха в квартире может варьироваться от 10 до 25 °C, в зависимости от назначения каждого отапливаемого помещения.

Жилые комнаты, к которым относятся гостиные, спальни кабинеты и подобные, должны быть нагреты до 22 °C. Возможно колебание этой отметки до 20 °C, особенно в холодных угловых помещениях. Максимальное значение термометра не должно превышать 24 °C.

Оптимальной считается температура от 19 до 21 °C, но допускается охлаждение зоны до 18 °C или интенсивный нагрев до 26 °C.

• Туалет повторяет температурный диапазон кухни. Но, ванная комната, или смежный санузел, считаются помещениями с повышенным уровнем влажности. Прогреваться эта часть квартиры может до 26 °C, а охлаждаться до 18 °C. Хотя, даже при оптимально допустимом значении в 20 °C использовать ванну по назначению неуютно.
• Комфортным диапазоном температуры для коридоров считается 18–20 °C. Но, уменьшение отметки до 16 °C признано вполне терпимым.
• Показатели в кладовых могут быть ещё ниже. Хотя оптимальные пределы — от 16 до 18 °C, отметки 12 или 22 °C не выходят за границы нормы.
• Войдя в подъезд, жилец дома может рассчитывать на температуру воздуха не ниже 16 °C.
• В лифте человек находится совсем недолго, отсюда и оптимальная температура всего в 5 °C.
• Самые холодные места многоэтажки — подвал и чердак. Температура здесь может понижаться до 4 °C.

Тепло в доме зависит и от времени суток. Официально признано, что во сне человек нуждается в меньшем количестве тепла. Исходя из этого, понижение температуры в комнатах на 3 градуса с 00.00 часов до 05.00 утра не считается нарушением.

Параметры температуры теплоносителя в системе отопления

Система отопления в многоквартирном доме – сложная структура, качественное функционирование которой зависит от правильности инженерных расчётов ещё на стадии проектирования.

Нагретый теплоноситель нужно не только доставить до здания с минимальными теплопотерями, но и равномерно распределить в помещениях на всех этажах.

Если в квартире холодно, то возможной причиной бывает проблема с сохранением необходимой температуры теплоносителя при перегоне.

Оптимальная и максимальная

Максимальная температура батарей рассчитана исходя из требований техники безопасности. Во избежание возгораний теплоноситель должен быть на 20 °C холоднее, чем температура, при которой некоторые материалы, способны самовоспламеняться. Норматив указывает на безопасные отметки в диапазоне от 65 до 115 °C.

Но, закипание жидкости внутри трубы крайне нежелательно, поэтому при превышении отметки в 105 °C может служить сигналом к принятию мер по остужению теплоносителя. Оптимальной для большинства систем считается температура в 75 °C. При превышении этой нормы, батарея оборудуется специальным ограничителем.

Минимальная

Максимально возможное охлаждение теплоносителя зависит от необходимой интенсивности прогрева помещения. Этот показатель напрямую связан с температурой воздуха на улице.

В зимнее время, при морозе в –20 °C, жидкость в радиаторе при начальной норме в 77 °C, не должна охлаждаться менее чем до 67 °C.

Нормальным значением в обратке при этом считается показатель в 70 °C. При потеплениях до 0 °C, температура теплоносителя может падать до 40–45 °C, а обратка до 35 °C.

Некоторые вопросы гидравлического расчёта тепловых сетей

В статье рассмотрено сопоставление инженерных формул для аналитического расчёта удельного гидравлического сопротивления трубопроводов водяных тепловых сетей и систем отопления для подтверждения их точности и области применения. Проведено сравнение различных подходов к определению оптимального диаметра теплопроводов и представлены особенности расчёта потерь давления на местных сопротивлениях в тепловых сетях.

Основной особенностью наружных тепловых сетей по сравнению с внутренними системами отопления являются значительно более высокие диаметры теплопроводов и, как следствие, другой режим течения воды, который, как правило, соответствует квадратичной области гидравлического сопротивления. Кроме того, в тепловых сетях оказывается также более высокой эквивалентная шероховатость стенок труб. В силу этого для гидравлического расчёта наружных сетей приходится применять несколько иные формулы и зависимости, чем для систем отопления зданий. При этом целесообразно сравнить результаты, даваемые каждой из этих зависимостей, для наглядного выявления различий в характере гидравлических сопротивлений, а также для дополнительной оценки точности используемых выражений и пределов их применимости.

В работе [1] автором приводится аппроксимационное соотношение для удельных потерь давления на трение R [Па/м] при движении воды в трубопроводах систем водяного отопления при использовании стальных водогазопроводных труб по ГОСТ 3262:

где w — скорость воды в трубопроводе, м/с; d_B — его внутренний диаметр, мм.

В то же время в публикации [2] показаны также выражения, которые могут применяться для гидравлического расчёта теплопроводов большого диаметра по ГОСТ 10704, используемых в наружных тепловых сетях.

Один из вариантов содержит зависимость R от расхода воды G [кг/ч]:

В силу определённых причин для гидравлического расчёта наружных сетей приходится применять несколько иные формулы и зависимости, чем для систем отопления зданий. При этом целесообразно сравнить результаты, даваемые каждой из этих зависимостей

Соотношение (2) справедливо при среднем значении плотности воды р = = 940 кг/м 3 , характерном для температур в теплосетях [3]. При других плотностях необходим пропорциональный пересчёт. С учётом связи между скоростью и расходом воды и сечением трубопровода получаем формулу в таком же виде, как и (1), но несколько отличающуюся числовыми коэффициентами:

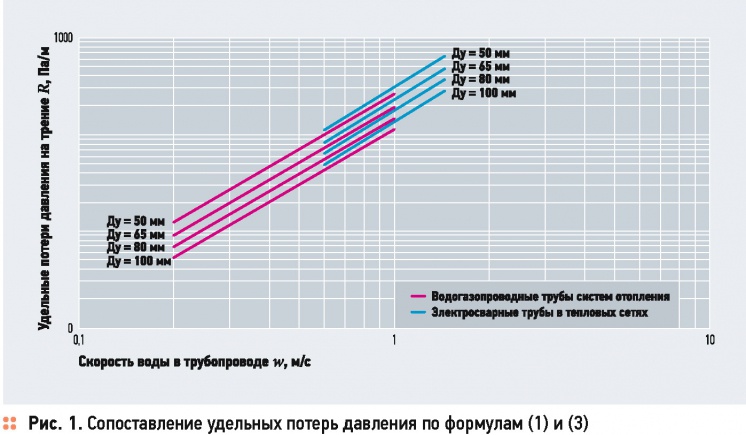
Сопоставление значений R, определяемых по формулам (1) и (3), можно наглядно показать с помощью рис. 1, где различные линии соответствуют как водогазопроводным трубам систем отопления, так и электросварным трубам в тепловых сетях. Для расчётов были выбраны четыре диаметра Dy50, Dy65, Dy80 и Dy100, являющиеся переходными между рассматриваемыми типами трубопроводов. Видно, что при скоростях в диапазоне 0,6—1,0 м/с удельные потери давления в обоих случаях изменяются практически одинаковым образом, но выражение (3) даёт величину R примерно на 16-20 % больше.

Это объясняется главным образом тем, что для теплосетей принята более высокая эквивалентная шероховатость труб, чем в системах водяного отопления, а именно — 0,5 вместо 0,2 мм [3, 4].

Заметим ещё, что в практике гидравлических расчётов тепловых сетей местные сопротивления принято учитывать в виде эквивалентных длин, то есть в виде добавки l_э к длине соответствующего участка теплопровода l. Из очевидного равенства величины потерь давления на местном сопротивлении ΔР_м = ζР_д = Rl_э, где ζ — коэффициент местного сопротивления (КМС), с учётом выражения для динамического давления Р_д = pw 1 2 3 4 5 6 /2 и для R из формулы (3), можно получить формулу для вычисления l_э:

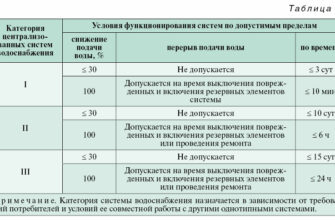
Как и в формуле (3), величину d_в необходимо здесь подставлять в [мм]. Значения КМС для различных сопротивлений можно принимать по справочным данным. В частности, для наиболее часто встречающихся случаев пересчётом из [3] можно получить табл. 1.

При этом, как было показано в работе [2], формула для экономически наиболее целесообразного диаметра трубопроводов теплосетей d_в.опт, при оптимальной скорости w_опт около 0,9 м/с, получается в следующем виде, где G следует подставлять в кг/ч:

Однако в работе [3] и некоторых других источниках рекомендуется при выборе диаметра трубопровода для заданного расхода учитывать, что величина R вдоль основного расчётного направления (то есть от источника теплоты до наиболее удалённого потребителя) должна составлять не более 80 Па/м. Если подставить данное значение в правую часть уравнения (2) и выразить оттуда d_в.опт, соответствующая формула будет выглядеть следующим образом:

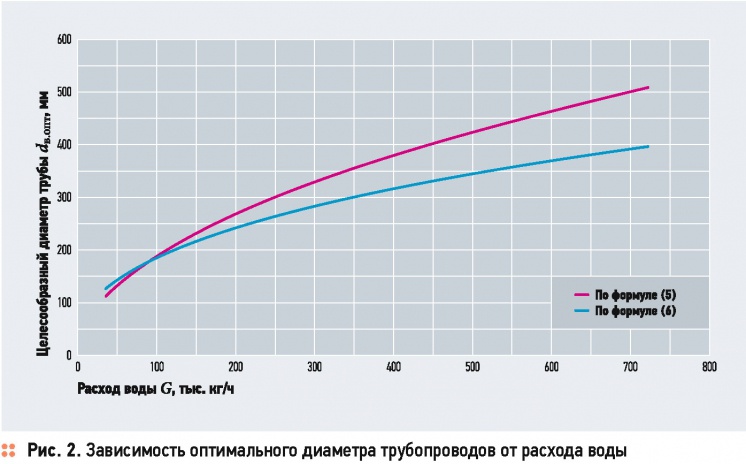
На рис. 2 приведено сопоставление результатов расчёта d_в.опт по выражениям (5) и (6). Видно, что оба подхода к выбору d_в.опт дают качественно близкие результаты. При этом экономически обоснованный уровень диаметра при средних и высоких расходах оказывается даже несколько выше, примерно на 15-20 %, что соответствует более низким значениям R — от 20 до 60 Па/м. В принципе, это не противоречит рекомендациям [3], поскольку величина 80 Па/м там обозначена как максимально допустимая. В настоящее время, однако, строительные нормативы требуют определять d_в.опт именно из технико-экономических соображений. В частности, такое указание имеется уже в документе [5], так что использование формулы (6) является наиболее обоснованным.

Заметим ещё, что во внутренних системах холодоснабжения при больших холодильных нагрузках диаметры трубопроводов также могут оказаться значительными и соответствующими условиям, рассматриваемым в данной работе. Тогда, если вместо воды используются низкозамерзающие холодоносители, в формулу (3) необходимо вводить поправочный коэффициент для учёта изменения физических свойств среды.

Из-за того, что режим течения в данном случае квадратичный, этот коэффициент будет равен только отношению плотности антифриза к плотности воды ρ_а / ρ, или, поскольку величина ρ считается равной 972 кг/м 3 [4], этот коэффициент допускается принимать по табл. 2, которую можно составить по данным работы [1] с учётом [6].

Таким образом, формулы и таблицы, приведённые в настоящей работе, очень просты, наглядны и доступны для инженерных расчётов, особенно при использовании электронных таблиц MS Excel, а также в учебном процессе. Они вполне обеспечивают требуемую точность в широком диапазоне скоростей и расходов воды и диаметрах вплоть до d_K = 325 мм. Этого вполне достаточно для проектирования водяных тепловых сетей в большинстве современных случаев.